题目内容

已知向量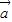=（sinθ，-2）与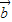=（1，cosθ）互相垂直，其中θ∈（0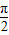，）．求：
（1）sinθ和cosθ的值
（2）tanθ的值．
【答案】分析：（1）由两向量的坐标及两向量垂直，利用平面向量的数量积运算法则列出关系式，再由同角三角函数间的基本关系列出关系式，联立两关系式即可求出sinθ和cosθ的值；
（2）利用同角三角函数公式即可求出tanθ的值．
解答：解：（1）由向量 =（sin θ，-2）与向量 =（1，cos θ）互相垂直，
得sinθ-2cosθ=0，又sin2θ+cos2θ=1，其中θ∈（0，），
解得：sinθ=，cosθ=；
（2）由tanθ=，得tanθ=2．
点评：此题考查了两角和与差的正弦、余弦函数公式，同角三角函数间的基本关系，以及特殊角的三角函数值，熟练掌握公式是解本题的关键．
练习册系列答案
相关题目
已知向量
a
=（sinβ，1），
b
=（2，-1）且
a
⊥
b
，
π
2
＜β＜π，则β等于
5
6
π
5
6
π
弧度．
已知向量
a
=（sinωx，-cosωx），
b
=（
3
cosωx，cosωx）（ω＞0），函数f（x）=
a
．
b
+
1
2
，且函数f（x）=
3
sinωxcosωx-cos2ωx+
1
2
的图象中任意两相邻对称轴间的距离为π．
（1）求ω的值；
（2）已知在△ABC中，角A，B，C所对的边分别为a，b，c，f（C）=
1
2
，且c=2
19
，△ABC的面积S=2
3
，求a+b的值．
已知向量
a
=（sinθ，cosθ-2sinθ），
b
=（1，2）
（1）若
a
⊥
b
，求tanθ的值；
（2）若
a
∥
b
，且θ为第Ⅲ象限角，求sinθ和cosθ的值．
（2013•德州二模）已知向量
a
=（sinα，1），
b
=（2，2cosα-
2
），（
π
2
＜α＜π），若
a
⊥
b
，则sin（α-
π
4
）=（　　）
已知向量
a
=（sinθ，1），
b
=（cosθ，
3
），且
a
∥
b
，其中θ∈（0，
π
2
）．
（1）求θ的值；
（2）若sin（x-θ）=
3
5
，0＜x＜
π
2
，求cosx的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网