题目内容
3.已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F2(1,0),点H(2,$\frac{2\sqrt{10}}{3}$)在椭圆上(Ⅰ)求椭圆的方程;
(Ⅱ)第一象限内一点M在圆C:x2+y2=b2上,过M作圆C的切线交椭圆于P,Q两点.问:△PF2Q的周长是否为定值,若是,求出定值,不是的话说明理由.
分析 (Ⅰ)椭圆的定义及两点之间的距离公式求得a的值,则b2=a2-c2=8,即可求得椭圆方程
(Ⅱ)将直线方程代入椭圆方程,利用韦达定理及弦长公式求得丨PQ丨,丨PF2丨,丨QF2丨,利用三角形的周长公式,即可求得答案.
解答 解:(Ⅰ)由椭圆的左焦点F1(-1,0),H在椭圆上,
丨HF1丨+丨HF2丨=2a,即$\sqrt{{3}^{2}+\frac{40}{9}}$+$\sqrt{1+\frac{40}{9}}$=6,
则a=3,c=1,b2=a2-c2=8,
∴椭圆的方程$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1$;
(Ⅰ)设PQ方程,y=kx+m,(k<0,m>0),A(x1,y1),B(x2,y2),
则PQ与C相切,
$\frac{m}{\sqrt{1+{k}^{2}}}$=2$\sqrt{2}$,m=2$\sqrt{2}$$\sqrt{1+{k}^{2}}$,
$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1}\end{array}\right.$,整理得:(8+9k2)x2+18kmx+9m2-72=0,
x1+x2=-$\frac{18km}{8+9{k}^{2}}$,x1x2=$\frac{9{m}^{2}-72}{8+9{k}^{2}}$,
丨PQ丨=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{4×9×8(4{k}^{2}-{m}^{2}+8)}{(8+9{k}^{2})^{2}}}$=-$\frac{6km}{8+9{k}^{2}}$,
丨PF2丨=$\sqrt{({x}_{1}-1)^{2}+{y}_{1}^{2}}$=$\sqrt{\frac{({x}_{1}-9)^{2}}{9}}$=3-$\frac{1}{3}$x1,
同理:丨QF2丨=3-$\frac{1}{3}$x2,
∴△PF2Q的周长S=丨PQ丨+丨PF2丨+丨QF2丨=6-$\frac{1}{3}$(x1+x2)-$\frac{6km}{8+9{k}^{2}}$=6,
∴△PF2Q的周长6.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,弦长公式,考查计算能力,属于中档题.

| 单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
| 销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(Ⅱ)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(Ⅰ)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{a}$+$\stackrel{∧}{b}$x的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{(x}_{i}-\overline{x}){(y}_{i}-\overline{y})}{{\sum_{i=1}^{n}{(x}_{i}-\overline{x})}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| A. | $\frac{{y}^{2}}{2}-\frac{{x}^{2}}{3}$=1 | B. | y2-$\frac{{x}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | $\frac{{y}^{2}}{3}-\frac{{x}^{2}}{2}$=1 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
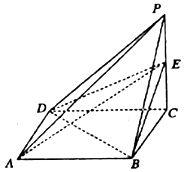 如图,已知四棱锥P-ABCD是边长为1的正方形,PB=PD=$\sqrt{5}$,PC=2,E是侧棱PC上的动点.
如图,已知四棱锥P-ABCD是边长为1的正方形,PB=PD=$\sqrt{5}$,PC=2,E是侧棱PC上的动点.