题目内容
3.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线为正方形OABC的边OA,OC所在的直线,点B为该双曲线的焦点.若正方形OABC的边长为2,则a=2.分析 根据双曲线渐近线在正方形的两个边,得到双曲线的渐近线互相垂直,即双曲线是等轴双曲线,结合等轴双曲线的性质进行求解即可.
解答  解:∵双曲线的渐近线为正方形OABC的边OA,OC所在的直线,
解:∵双曲线的渐近线为正方形OABC的边OA,OC所在的直线,
∴渐近线互相垂直,则双曲线为等轴双曲线,即渐近线方程为y=±x,
即a=b,
∵正方形OABC的边长为2,
∴OB=2$\sqrt{2}$,即c=2$\sqrt{2}$,
则a2+b2=c2=8,
即2a2=8,
则a2=4,a=2,
故答案为:2
点评 本题主要考查双曲线的性质的应用,根据双曲线渐近线垂直关系得到双曲线是等轴双曲线是解决本题的关键.

练习册系列答案
相关题目
11.某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
(I)记A为事件:“一续保人本年度的保费不高于基本保费”.求P(A)的估计值;
(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;
(Ⅲ)求续保人本年度的平均保费估计值.
| 上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
| 出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;
(Ⅲ)求续保人本年度的平均保费估计值.
18.某三棱锥的三视图如图所示,则该三棱锥的体积为( )


| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
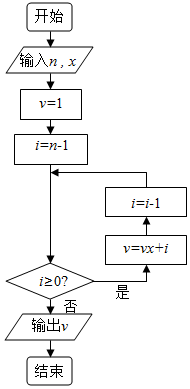 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( )