题目内容
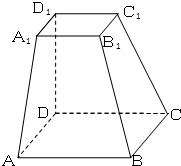
如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°,
(Ⅰ)证明:AA1⊥BD;
(Ⅱ)证明:CC1∥平面A1BD。
(Ⅰ)证明:AA1⊥BD;
(Ⅱ)证明:CC1∥平面A1BD。

证明:(Ⅰ)因为AB=2AD,所以设AD=a,则AB=2a,
又因为∠BAD=60°,
所以在△ABD中,由余弦定理得: ,
,
所以BD= ,
,
所以 ,故BD⊥AD,
,故BD⊥AD,
又因为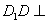 平面ABCD,
平面ABCD,
所以D1D⊥BD,
又因为AD∩D1D=D,
所以BD⊥平面ADD1A1,故 。
。
(2)连结AC,设AC∩BD=O,连结 ,
,
由底面ABCD是平行四边形得:O是AC的中点,
由四棱台 知:平面ABCD∥平面
知:平面ABCD∥平面 ,
,
因为这两个平面同时都和平面 相交,交线分别为AC、
相交,交线分别为AC、 ,故
,故 ,
,
又因为AB=2a,BC=a, ,
,
所以可由余弦定理计算得AC= ,
,
又因为A1B1=2a,B1C1= ,
, ,
,
所以可由余弦定理计算得A1C1= ,
,
所以A1C1∥OC且A1C1=OC,
故四边形OCC1A1是平行四边形,所以CC1∥A1O,
又CC1 平面A1BD,A1O
平面A1BD,A1O 平面A1BD,
平面A1BD,
所以CC1∥平面A1BD。
又因为∠BAD=60°,
所以在△ABD中,由余弦定理得:
 ,
,所以BD=
 ,
,所以
 ,故BD⊥AD,
,故BD⊥AD,又因为
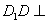 平面ABCD,
平面ABCD,所以D1D⊥BD,
又因为AD∩D1D=D,
所以BD⊥平面ADD1A1,故
 。
。(2)连结AC,设AC∩BD=O,连结
 ,
,由底面ABCD是平行四边形得:O是AC的中点,
由四棱台
 知:平面ABCD∥平面
知:平面ABCD∥平面 ,
,因为这两个平面同时都和平面
 相交,交线分别为AC、
相交,交线分别为AC、 ,故
,故 ,
,又因为AB=2a,BC=a,
 ,
,所以可由余弦定理计算得AC=
 ,
,又因为A1B1=2a,B1C1=
 ,
, ,
,所以可由余弦定理计算得A1C1=
 ,
,所以A1C1∥OC且A1C1=OC,
故四边形OCC1A1是平行四边形,所以CC1∥A1O,
又CC1
 平面A1BD,A1O
平面A1BD,A1O 平面A1BD,
平面A1BD,所以CC1∥平面A1BD。

练习册系列答案
相关题目
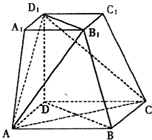 如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.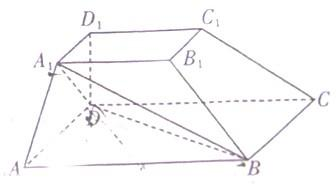
 如图:在四棱台ABCD-A1B1C1D1中,DD1垂直底面,且DD1=2,底面四边形ABCD与A1B1C1D1分别为边长2和1的正方形.
如图:在四棱台ABCD-A1B1C1D1中,DD1垂直底面,且DD1=2,底面四边形ABCD与A1B1C1D1分别为边长2和1的正方形. (2009•聊城一模)如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
(2009•聊城一模)如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.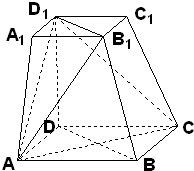 用平行于棱锥底面的平面去截棱锥,则截面与底面之间的部分叫棱台.如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
用平行于棱锥底面的平面去截棱锥,则截面与底面之间的部分叫棱台.如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.