题目内容
函数 .
.
(1)若 ,函数
,函数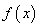 在区间
在区间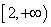 上是单调递增函数,求实数
上是单调递增函数,求实数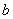 的取值范围;
的取值范围;
(2)设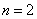 ,若对任意
,若对任意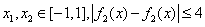 恒成立,求
恒成立,求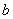 的取值范围.
的取值范围.
解: (1) 时,
时,
任设 ,
,

 ,
,
因为函数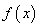 在
在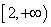 上是单调递增函数,故恒有
上是单调递增函数,故恒有 ,..3分
,..3分
从而恒有 ,即恒有
,即恒有 ,
,
当 时,
时, ,
, ,
,
(2)当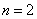 时
时
对任意 有
有 恒成立等价于
恒成立等价于 在
在 上的最大值与最小值之差
上的最大值与最小值之差
当 ,即
,即 时,
时, 在
在 上单调递增,
上单调递增,
所以 ,
, ,所以
,所以 ,与题设矛盾;
,与题设矛盾;
当 ,即
,即 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增,所以
上单调递增,所以 ,
, ,
,
所以 恒成立,所以
恒成立,所以 ;
;
当 ,即
,即 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增,所以
上单调递增,所以 ,
, ,
,
所以 恒成立,所以
恒成立,所以 ;
;
当 ,即
,即 时,
时, 在
在 上单调递减,
上单调递减,
所以 ,
, ,所以
,所以 ,与题设矛盾.
,与题设矛盾.
综上所述,实数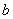 的取值范围是
的取值范围是 .…
.…

练习册系列答案
相关题目
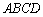 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛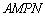 ,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过点C。已知AB=2米,AD=1米。
,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过点C。已知AB=2米,AD=1米。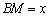 (单位:米),要使花坛AMPN的面积大于9
(单位:米),要使花坛AMPN的面积大于9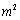 ,求
,求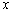 的取值范围。
的取值范围。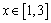 (单位:米),则当AM,AN的长分别是多少时,花坛AMPN的面积最大?并求出最大面积。
(单位:米),则当AM,AN的长分别是多少时,花坛AMPN的面积最大?并求出最大面积。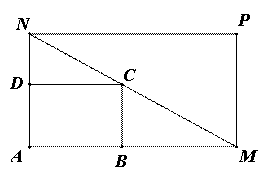
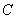 的内接正方形相对的两个顶点的坐标分别为
的内接正方形相对的两个顶点的坐标分别为
 的直线与圆
的直线与圆 的方程
的方程 在一个周期内的图象,则其解析式是______ ______.
在一个周期内的图象,则其解析式是______ ______.

 .
. 的值;
的值; ,求
,求 的值;
的值;
 的左、右焦点分别为
的左、右焦点分别为 ,渐近线分别为
,渐近线分别为 ,点P在第一象限内且在
,点P在第一象限内且在 上,若
上,若 ,
, ,则双曲线的离心率为 .
,则双曲线的离心率为 . 到点
到点 的距离等于它到直线
的距离等于它到直线 的距离,则点
的距离,则点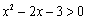 ”是 “
”是 “ ”的必要不充分条件,则
”的必要不充分条件,则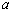 的最大值为 .
的最大值为 .