Question

将函数f（x）=cos（π+x）（cosx-2sinx）+sin²x的图象向左平移

π

8

后得到函数g（x），则g（x）具有性质（　　）

A．最大值为 2 ，图象关于直线x= π 2 对称

B．周期为π，图象关于( π 4 ，0)对称

C．在(- π 2 ，0)上单调递增，为偶函数

D．在(0， π 4 )上单调递增，为奇函数

Answer 1

函数f（x）=cos（π+x）（cosx-2sinx）+sin²x=-cosx（cosx-2sinx）+sin²x
=-cos2x+sin2x=

2

sin（2x-

π

4

），
把函数f（x）的图象向左平移

π

8

后得到函数g（x）=

2

sin[2（x+

π

8

）-

π

4

]=

2

sin2x 的图象，
故函数g（x）在(0，

π

4

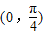)上单调递增，为奇函数，
故选D．