题目内容
（选做1）设a，b，c都为正数，求证：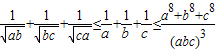
．
【答案】分析：根据所要证不等式的特点，先证明一个结论：当x＞0，y＞0，z＞0时，有x2+y2+z2≥xy+yz+xz，令x=
，y=
，z=
，得：
；同理：
，再继续利用上述结论即可证得结论．
解答：解：当x＞0，y＞0，z＞0时，有x2+y2≥2xy，x2+z2≥2xz，y2+z2≥2yz，
∴2（x2+y2+z2）≥2（xy+yz+xz），∴x2+y2+z2≥xy+yz+xz，
令x=
，y=
，z=
，得：
；
同理：
≥
=
=a2+b2+c2≥ab+bc+ca，
∴
=
．
综上所述，
．
点评：本小题主要考查不等式的证明、基本不等式等基础知识，考查运算求解能力，考查化归与转化思想．属于基础题．
，y=，z=，得：；同理：，再继续利用上述结论即可证得结论．解答：解：当x＞0，y＞0，z＞0时，有x2+y2≥2xy，x2+z2≥2xz，y2+z2≥2yz，
∴2（x2+y2+z2）≥2（xy+yz+xz），∴x2+y2+z2≥xy+yz+xz，
令x=
，y=，z=，得：；同理：
≥=
=a2+b2+c2≥ab+bc+ca，∴
=．综上所述，
．点评：本小题主要考查不等式的证明、基本不等式等基础知识，考查运算求解能力，考查化归与转化思想．属于基础题．
练习册系列答案
相关题目
选做题：在A、B、C、D四小题中只能选做2题，每小题10分，共20分．解答应写出文字说明、证明过程或演算步骤．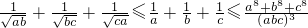
．