题目内容
(选做1)设a,b,c都为正数,求证:
+
+
≤
+
+
≤
.
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| a8+b8+c8 |
| (abc)3 |
分析:根据所要证不等式的特点,先证明一个结论:当x>0,y>0,z>0时,有x2+y2+z2≥xy+yz+xz,令x=
,y=
,z=
,得:
+
+
≥
+
+
;同理:
≥
,再继续利用上述结论即可证得结论.
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| a8+b8+c8 |
| (abc)2 |
| a4b 4+b4c 4+c4a 4 |
| (abc)2 |
解答:解:当x>0,y>0,z>0时,有x2+y2≥2xy,x2+z2≥2xz,y2+z2≥2yz,
∴2(x2+y2+z2)≥2(xy+yz+xz),∴x2+y2+z2≥xy+yz+xz,
令x=
,y=
,z=
,得:
+
+
≥
+
+
;
同理:
≥
≥
=
=a2+b2+c2≥ab+bc+ca,
∴
≥
=
+
+
.
综上所述,
+
+
≤
+
+
≤
.
∴2(x2+y2+z2)≥2(xy+yz+xz),∴x2+y2+z2≥xy+yz+xz,
令x=
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
同理:
| a8+b8+c8 |
| (abc)2 |
| a4b 4+b4c 4+c4a 4 |
| (abc)2 |
| a2b 4c 2+a 4b2c 2+c4a 2b 2 |
| (abc)2 |
=
| a2b 2c 2(a 2+b2 +c2 ) |
| (abc)2 |
∴
| a8+b8+c8 |
| (abc)3 |
| ab+bc+ca |
| abc |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
综上所述,
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| a8+b8+c8 |
| (abc)3 |
点评:本小题主要考查不等式的证明、基本不等式等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.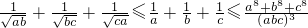 .
.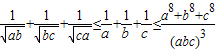 .
.