题目内容
设A>0,求函数f(x)=![]() -1n(x+A)(x∈(0,+∞))的单调区间.
-1n(x+A)(x∈(0,+∞))的单调区间.
答案:
解析:
解析:
f'(x)= 当A>0,x>0时, f'(x)>0 f'(x)<0 ①当A>1时,对所有x>0,有x2+(2A-4)x+A2>0, 即f'(x)>0. 此时f'(x)在(0,+∞)内单调递增. ②当A=1时,对x≠1,有x2+(2A-4)x+A2>0, 即f'(x)>0此时f'(x)在(0,1)内单调递增,在(1,+∞)内单调递增. 又知函数f(x)在x=1处连续. 因此,函数f(x)在(0,+∞)内单调递增. ③当0<A>1时,令f'(x)>0,即x2+(2A-4)x+A2>0,解得,x<2-A-2 因此,函数f(x)在区间(0,2-A-2 令f'(x)<0,即x2+(2A-4)x+A2<0,解得2-A-2 因此,函数f(x)在区间(2-A-2 |

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
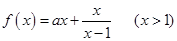
 的最小值;
的最小值;