题目内容

已知a=(cosα,sinα),b=(cosβ,sinβ)(a≠b).

求证:(a+b)⊥(a-b).

剖析:只要证(a+b)·(a-b)=0即可.

证法一:(a+b)·(a-b)=|a|2-|b|2=1-1=0,∴(a+b)⊥(a-b).

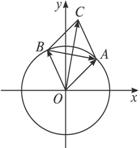
证法二:在单位圆中设=a,=b,以、为邻边作OACB,

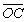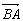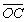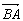则OACB为菱形.∴Equation.3⊥Equation.3.

    ∴Equation.3·Equation.3=0,

    即(a+b)·(a-b)=0.

    ∴(a+b)⊥(a-b).


练习册系列答案
相关题目
已知
a
=(cosα，sinα)，
b
=(cosβ，sinβ)，其中0＜α＜β＜π．
（1）求证：
a
+
b
与
a
-
b
互相垂直；
（2）若k
a
+
.
b
与
a
-k
.
b
的长度相等，求α-β的值（k为非零的常数）．
（2008•静安区一模）（文）已知
a
=(cosα，3sinα)，
b
=(3cosβ，sinβ)，(0＜β＜α＜
π
2
)是平面上的两个向量．
（1）试用α、β表示
a
•
b
；
（2）若
a
•
b
=
36
13
，且cosβ=
4
5
，求α的值（结果用反三角函数值表示）
已知
a
=(cosθ，sinθ)，
b
=(cosα，sinα)，则下列说法不正确的是（　　）
已知
a
=
cosωx，sinωx
，
b
=
cosωx+
3
sinωx，
3
cosωx-sinωx
（ω＞0），函数f(x)=
a
•
b
的最小正周期为π
（1）求函数f（x）的单调递减区间及对称中心；
（2）求函数f（x）在区间
π
4
，
π
2
上的最大值与最小值．
（2005•朝阳区一模）已知
a
=(cosα，sinα)，
b
=(cosβ，sinβ)，0＜α＜β＜π
（I）求|
a
|的值；
（II）求证：
a
+
b
与
a
-
b
互相垂直；
（III）设|k
a
+
b
|=|
a
-k
b
|，k∈R且k≠0，求β-α的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网