题目内容
13．若x，y满足约束条件$\left\{\begin{array}{l}2x-y-1≤0\\ 2x+y-7≤0\\ x≥1\end{array}\right.$则$\frac{y}{x+1}$的取值范围为$[{\frac{1}{2}，\frac{5}{2}}]$．分析 作出不等式组对应的平面区域，利用目标函数的几何意义，进行求解即可．
解答 
解：作出不等式组约束条件$\left\{\begin{array}{l}2x-y-1≤0\\ 2x+y-7≤0\\ x≥1\end{array}\right.$对应的平面区域如图：z=$\frac{y}{x+1}$，
则z的几何意义为区域内的点（-1，0）的斜率，
由图象知z的最小为DA的斜率：$\frac{1}{2}$，z的最大值为BD的斜率：$\frac{5}{1+!}$=$\frac{5}{2}$，
则$\frac{1}{2}$≤z≤2，
故答案为：$[{\frac{1}{2}，\frac{5}{2}}]$．
点评 本题主要考查线性规划和直线斜率的基本应用，利用目标函数的几何意义和数形结合是解决问题的基本方法．
练习册系列答案
相关题目
8．已知函数f（x）=2sin（ωx+φ）-1（ω＞0，|φ|＜π）的一个零点是$x=\frac{π}{3}$，$x=-\frac{π}{6}$是y=f（x）的图象的一条对称轴，则ω取最小值时，f（x）的单调增区间是（ ）
| A． | $[{-\frac{7}{3}π+3kπ，-\frac{1}{6}π+3kπ}]，k∈Z$ | B． | $[{-\frac{5}{3}π+3kπ，-\frac{1}{6}π+3kπ}]，k∈Z$ | ||
| C． | $[{-\frac{2}{3}π+2kπ，-\frac{1}{6}π+2kπ}]，k∈Z$ | D． | $[{-\frac{1}{3}π+2kπ，-\frac{1}{6}π+2kπ}]，k∈Z$ |
5．
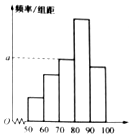某教师为了分析所任教班级某将考试的成绩，将全班同学的成绩做出了频数与频率的统计表和频率分布直方图．
（1）求表中t，q及图中a的值；
（2）该教师从这次考试成绩低于70分的学生中随机抽取3人进行面批，设X表示所抽取学生中成绩低于60分的人数，求随机变量X的分布列和数学期望．
某教师为了分析所任教班级某将考试的成绩，将全班同学的成绩做出了频数与频率的统计表和频率分布直方图．| 分组 | 频数 | 频率 |
| [50，60） | 3 | 0.06 |
| [60，70） | m | 0.10 |
| [70，80） | 13 | n |
| [80，90） | p | q |
| [90，100] | 9 | 0.18 |
| 总计 | t | 1 |
（2）该教师从这次考试成绩低于70分的学生中随机抽取3人进行面批，设X表示所抽取学生中成绩低于60分的人数，求随机变量X的分布列和数学期望．