题目内容

如图，平行四边形ABCD中，M是DC的中点，N在线段BC上，且NC=2BN．已知
AM
=
c
，
AN
=
d
，试用
c
，
d
表示
AB
和
AD
．
分析：根据向量加法的三角形法则及已知条件，可得
AM
=
AD
+
1
2
AB
．
AN
=
AB
+
1
3
AD
．由
AM
=
c
，
AN
=
d
，构造方程组
c
=
1
2
AB
+
AD
，
d
=
AB
+
1
3
AD
．进而可将
AB
和
AD
用
c
和
d
表示．
解答：解：因为四边形ABCD为平行四这形，
M为DC的中点，NC=2BN，
所以
AM
=
AD
+
DM
=
AD
+
1
2
AB
．
AN
=
AB
+
BN
=
AB
+
1
3
AD
．
因为
AM
=
c
，
AN
=
d
，
所以
c
=
1
2
AB
+
AD
．
d
=
AB
+
1
3
AD
．
解得
AB
=
2
5
（3
d
-
c
），
AD
=
3
5
（2
c
-
d
）．
点评：本题考查的知识点是向量加法的三角形法则，其中由已知得到
AM
=
AD
+
1
2
AB
．
AN
=
AB
+
1
3
AD
．是解答的关键．
练习册系列答案
相关题目
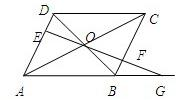精英家教网如图，平行四边形ABCD的对角线交于点O，过点O的直线交AD于E，BC于F，交AB延长线于G，已知AB=a，BC=b，BG=c，则BF=
 
．
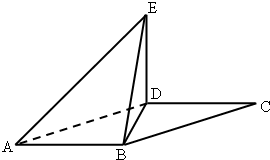精英家教网如图，平行四边形ABCD中，∠DAB=60°，AB=2，AD=4将△CBD沿BD折起到△EBD的位置，使平面EDB⊥平面ABD．
（I）求证：AB⊥DE
（Ⅱ）求三棱锥E-ABD的侧面积．
如图，平行四边形ABCD中，E，F分别是BC，DC的中点，G为交点，若
AB
=
a
，
AD
=
b
，试以
a
，
b
为基底表示
CG
=
-
1
3
(
a
+
b
)
-
1
3
(
a
+
b
)
．
（2012•枣庄一模）如图，平行四边形ABCD中，点E是边BC（靠近点B）的三等分点，F是AB（靠近点A）的三等分点，P是AE与DF的交点，则
AP
用
AB
，
AD
表示为
AP
=
3
10
AB
+
1
10
AD
AP
=
3
10
AB
+
1
10
AD
．
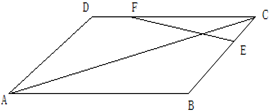精英家教网如图，平行四边形ABCD中，
AB
=
a
，
AD
=
b
，
CE
=
1
3
CB
，
CF
=
2
3
CD
．
（1）用
a
，
b
表示
EF
；
（2）若|
a
|=1，|
b
|=4，∠DAB=60°，分别求|
EF
|和
AC
•
FE
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网