题目内容
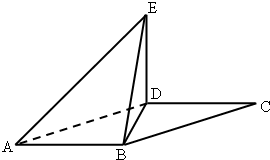 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.
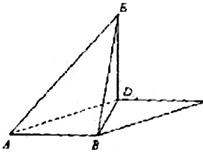
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.(I)求证:AB⊥DE
(Ⅱ)求三棱锥E-ABD的侧面积.
分析:(I)要证:AB⊥DE,容易推出AB⊥BD,可证明AB⊥平面EBD即可.
(Ⅱ)求三棱锥E-ABD的侧面积,需要求出三个侧面三角形的面积即可.
(Ⅱ)求三棱锥E-ABD的侧面积,需要求出三个侧面三角形的面积即可.
解答:解:(I)证明:在△ABD中,∵AB=2,AD=4,∠DAB=60°
∴BD=
=2
∴AB2+BD2=AD2,∴AB⊥DB,
又∵平面EBD⊥平面ABD
平面EBD∩平面ABD=BD,AB?平面ABD,∴AB⊥平面EBD,
∵DE?平面EBD,∴AB⊥DE.
(Ⅱ)解:由(I)知AB⊥BD,CD∥AB,∴CD⊥BD,从而DE⊥DB
在Rt△DBE中,∵DB=2
,DE=DC=AB=2
∴S△DBE=
DB•DE=2
又∵AB⊥平面EBD,BE?平面EBD,
∴AB⊥BE,
∵BE=BC=AD=4,∴S△ABE=
AB•BE=4,
∵DE⊥BD,平面EBD⊥平面ABD∴ED⊥平面ABD
而AD?平面ABD,∴ED⊥AD,∴S△ADE=
AD•DE=4
综上,三棱锥E-ABD的侧面积,S=8+2
∴BD=
| AB2+AD2-2AB•2ADcos∠DAB |
| 3 |

∴AB2+BD2=AD2,∴AB⊥DB,
又∵平面EBD⊥平面ABD
平面EBD∩平面ABD=BD,AB?平面ABD,∴AB⊥平面EBD,
∵DE?平面EBD,∴AB⊥DE.
(Ⅱ)解:由(I)知AB⊥BD,CD∥AB,∴CD⊥BD,从而DE⊥DB
在Rt△DBE中,∵DB=2
| 3 |
∴S△DBE=
| 1 |
| 2 |
| 3 |
又∵AB⊥平面EBD,BE?平面EBD,
∴AB⊥BE,
∵BE=BC=AD=4,∴S△ABE=
| 1 |
| 2 |
∵DE⊥BD,平面EBD⊥平面ABD∴ED⊥平面ABD
而AD?平面ABD,∴ED⊥AD,∴S△ADE=
| 1 |
| 2 |
综上,三棱锥E-ABD的侧面积,S=8+2
| 3 |
点评:本题考查棱锥的侧面积,直线和直线的垂直,是中档题.

练习册系列答案
相关题目
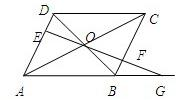 如图,平行四边形ABCD的对角线交于点O,过点O的直线交AD于E,BC于F,交AB延长线于G,已知AB=a,BC=b,BG=c,则BF=
如图,平行四边形ABCD的对角线交于点O,过点O的直线交AD于E,BC于F,交AB延长线于G,已知AB=a,BC=b,BG=c,则BF= 如图,平行四边形ABCD中,E,F分别是BC,DC的中点,G为交点,若
如图,平行四边形ABCD中,E,F分别是BC,DC的中点,G为交点,若 (2012•枣庄一模)如图,平行四边形ABCD中,点E是边BC(靠近点B)的三等分点,F是AB(靠近点A)的三等分点,P是AE与DF的交点,则
(2012•枣庄一模)如图,平行四边形ABCD中,点E是边BC(靠近点B)的三等分点,F是AB(靠近点A)的三等分点,P是AE与DF的交点,则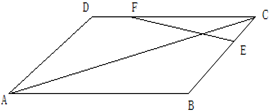 如图,平行四边形ABCD中,
如图,平行四边形ABCD中,