题目内容
已知△ABC的顶点A(5,1),AB边上的高CH所在的直线方程为2x-y-5=0,AC边上的中线BM所在的直线方程为x-2y-5=0.(1)求顶点B的坐标;
(2)求直线BC的方程.
【答案】分析:(Ⅰ)由AB边上的高CH所在直线方程为2x-y-5=0可得直线CH的斜率为2,根据垂直时斜率乘积为-1可得直线AB的斜率为- ,且过(5,1)即可得到AB边所在直线方程,然后联立解方程组即可.
,且过(5,1)即可得到AB边所在直线方程,然后联立解方程组即可.
(2)设出点C的坐标,即可得出中点M的坐标,然后代入x-2y-5=0,从而求出C的坐标,即可得出直线方程.
解答:解:(Ⅰ)由AB边上的高CH所在直线方程为2x-y-5=0可知kAB=- ,
,
又A(5,1),AB边所在直线方程为y-1=- (x-5)①
(x-5)①
∵BM所在的直线方程为x-2y-5=0②
联立①②解得:x=6,y=
∴B(6, )
)
(2)设(x,yo),则AC的中点M(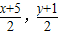 )在中线BM上,即
)在中线BM上,即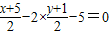 又点C在高CH上,得2x-y-5=0
又点C在高CH上,得2x-y-5=0
联立解得x=1,y=-3
即C(1,-3)
故直线BC的方程为7x-10y-37=0
点评:考查学生掌握两直线垂直时满足斜率乘积为-1的条件,会求两直线的交点坐标,以及会根据斜率和一点坐标写出直线的一般式方程.
 ,且过(5,1)即可得到AB边所在直线方程,然后联立解方程组即可.
,且过(5,1)即可得到AB边所在直线方程,然后联立解方程组即可.(2)设出点C的坐标,即可得出中点M的坐标,然后代入x-2y-5=0,从而求出C的坐标,即可得出直线方程.
解答:解:(Ⅰ)由AB边上的高CH所在直线方程为2x-y-5=0可知kAB=-
 ,
,又A(5,1),AB边所在直线方程为y-1=-
 (x-5)①
(x-5)①∵BM所在的直线方程为x-2y-5=0②
联立①②解得:x=6,y=

∴B(6,
 )
)(2)设(x,yo),则AC的中点M(
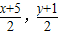 )在中线BM上,即
)在中线BM上,即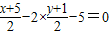 又点C在高CH上,得2x-y-5=0
又点C在高CH上,得2x-y-5=0联立解得x=1,y=-3
即C(1,-3)
故直线BC的方程为7x-10y-37=0
点评:考查学生掌握两直线垂直时满足斜率乘积为-1的条件,会求两直线的交点坐标,以及会根据斜率和一点坐标写出直线的一般式方程.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目