题目内容
已知函数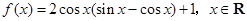 .
.
(1)求函数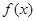 的单调递增取区间;
的单调递增取区间;
(2)将函数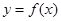 的图象向左平移
的图象向左平移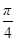 个单位后,再将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位后,再将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数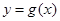 的图象,求
的图象,求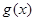 的最大值及取得最大值时的
的最大值及取得最大值时的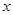 的集合.
的集合.
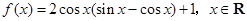 .
.(1)求函数
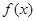 的单调递增取区间;
的单调递增取区间;(2)将函数
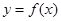 的图象向左平移
的图象向左平移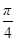 个单位后,再将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位后,再将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数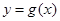 的图象,求
的图象,求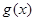 的最大值及取得最大值时的
的最大值及取得最大值时的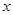 的集合.
的集合.(1)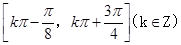 ;(2)
;(2)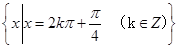 ,
,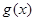 的最大值为
的最大值为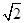 .
.
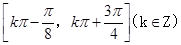 ;(2)
;(2)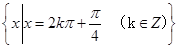 ,
,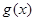 的最大值为
的最大值为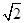 .
.(1)先化简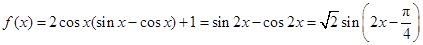 ,
,
再由 即得
即得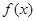 递增区间为
递增区间为 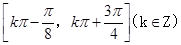 .
.
(2)由已知,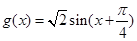 .
.
解:(1)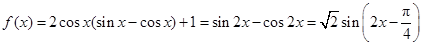 ,
,
当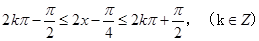 即
即 ,
,
因此,函数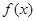 的单调递增区间为
的单调递增区间为 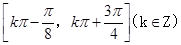 .
.
(2)由已知,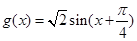 ,
,
∴当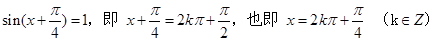 时,
时,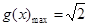 .
.
∴ 当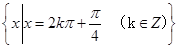 ,
,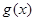 的最大值为
的最大值为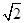 .
.
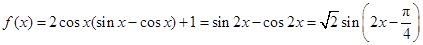 ,
, 再由
 即得
即得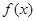 递增区间为
递增区间为 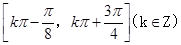 .
.(2)由已知,
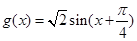 .
.解:(1)
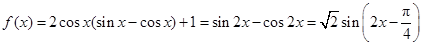 ,
, 当
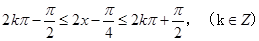 即
即 ,
,因此,函数
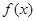 的单调递增区间为
的单调递增区间为 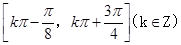 .
.(2)由已知,
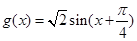 ,
,∴当
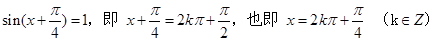 时,
时,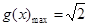 .
.∴ 当
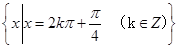 ,
,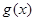 的最大值为
的最大值为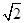 .
.
练习册系列答案
相关题目

 +b的形式,并用五点法作出函数f(x)在一个周期上的简图;
+b的形式,并用五点法作出函数f(x)在一个周期上的简图;
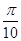 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是( )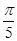 )
)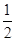 x-
x- )
)
 ,
,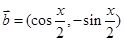 ,且
,且 ,
, (
( 为常数),求:
为常数),求: 及
及 ;
; 的最小值是
的最小值是 ,求实数
,求实数
 在区间
在区间 上的图象;
上的图象; 在区间
在区间 的取值范围.
的取值范围. 角的直路
角的直路 ,交点为
,交点为 ,甲、乙分别在
,甲、乙分别在 上,起初甲离
上,起初甲离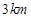 ,乙离
,乙离 ,后来甲沿
,后来甲沿 的方向,乙沿
的方向,乙沿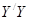 的方向,同时以
的方向,同时以 的速度步行。
的速度步行。 小时后两人的距离是多少?
小时后两人的距离是多少?
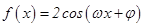 (
(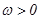 且
且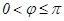 )为奇函数,其图象与
)为奇函数,其图象与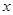 轴的所有交点中最近的两交点间的距离为
轴的所有交点中最近的两交点间的距离为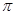 ,则
,则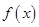 的一个单调递增区间为 ( )
的一个单调递增区间为 ( )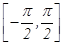
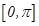
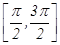
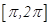
 的最小正周期为
的最小正周期为  的图像向右平移
的图像向右平移 个单位,再向上平移2个单位所得图像对应的函数解析式是( )
个单位,再向上平移2个单位所得图像对应的函数解析式是( )


