题目内容
设函数f(x)=kx3+3(k-1)x2-k2+1的极值点是0和4.
(1)求常数k的值;
(2)确定函数f(x)的单调区间;
(3)求f(x)的极值.
解:(1)f′(x)=3kx2+6(k-1)x,由于极值点是0和4,
∴0和4是方程3kx2+6(k-1)x=0的两根,可求得 ;
;
(2)由(1)可知f′(x)=3kx2+6(k-1)x=x2-4x=x(x-4),
∴当x<0或x>4,f(x)为增函数,
0≤x≤4,f(x)为减函数;
(3)由(2)可判断极大值为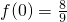 ,极小值为
,极小值为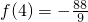 .
.
分析:(1)因为函数两个极值点已知,令f′(x)=3kx2+6(k-1)x=0,把0和4代入求出k即可.
(2)利用函数的导数确定函数的单调区间,f′(x)=3kx2+6(k-1)x=x2-4x=x(x-4)大于零和小于零分别求出递增和递减区间即可.
(3)把函数驻点带到f(x)中,判断极大极小值即可.
点评:考查学生利用导数研究函数的单调性的能力,理解函数驻点的意义.
∴0和4是方程3kx2+6(k-1)x=0的两根,可求得
 ;
;(2)由(1)可知f′(x)=3kx2+6(k-1)x=x2-4x=x(x-4),
∴当x<0或x>4,f(x)为增函数,
0≤x≤4,f(x)为减函数;
(3)由(2)可判断极大值为
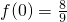 ,极小值为
,极小值为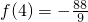 .
.分析:(1)因为函数两个极值点已知,令f′(x)=3kx2+6(k-1)x=0,把0和4代入求出k即可.
(2)利用函数的导数确定函数的单调区间,f′(x)=3kx2+6(k-1)x=x2-4x=x(x-4)大于零和小于零分别求出递增和递减区间即可.
(3)把函数驻点带到f(x)中,判断极大极小值即可.
点评:考查学生利用导数研究函数的单调性的能力,理解函数驻点的意义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
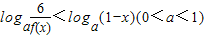 的解集.
的解集.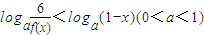 的解集.
的解集.