题目内容
等差数列{an}满足a1>0,3a4=7a7,若前n项和Sn取得最大值,则n=( )A.8
B.9
C.10
D.11
【答案】分析:把a1和d代入3a4=7a7,求得a1=-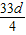 ,进而可判断a9>0,a10<0,故可知数列前9项均为正数,进而可知答案.
,进而可判断a9>0,a10<0,故可知数列前9项均为正数,进而可知答案.
解答:解:设等差数列{an}的公差为d,∵足a1>0,且3a4=7a7,
∴3(a1+3d)=7(a1+6d),化简可得 4a1+33d=0.
即 a1=-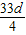 ,可得d<0,
,可得d<0,
∴a9=a1+8d>0,a10=a1+9d<0,
∴前9项和最大.
故选B.
点评:本题考查等差数列的性质,利用数列的单调性时解决问题的关键,属基础题.
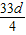 ,进而可判断a9>0,a10<0,故可知数列前9项均为正数,进而可知答案.
,进而可判断a9>0,a10<0,故可知数列前9项均为正数,进而可知答案.解答:解:设等差数列{an}的公差为d,∵足a1>0,且3a4=7a7,
∴3(a1+3d)=7(a1+6d),化简可得 4a1+33d=0.
即 a1=-
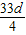 ,可得d<0,
,可得d<0,∴a9=a1+8d>0,a10=a1+9d<0,
∴前9项和最大.
故选B.
点评:本题考查等差数列的性质,利用数列的单调性时解决问题的关键,属基础题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目