题目内容
设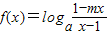 为奇函数,
为奇函数,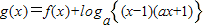 (a>1且m≠1)
(a>1且m≠1)(1)求m的值及g(x)的定义域;
(2)若g(x)在
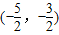 上恒为正,求a的取值范围.
上恒为正,求a的取值范围.
【答案】分析:(1)根据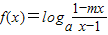 为奇函数,f(x)+f(-x)=0,结合对数的运算性质,可得m2=1,结合m≠1得m=-1,进而根据对数函数真数大于0,构造不等式组,求出函数的定义域.
为奇函数,f(x)+f(-x)=0,结合对数的运算性质,可得m2=1,结合m≠1得m=-1,进而根据对数函数真数大于0,构造不等式组,求出函数的定义域.
(2)根据g(x)在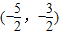 上恒为正,结合底数大于1,可得真数恒大于1,进而a>-
上恒为正,结合底数大于1,可得真数恒大于1,进而a>-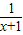 ,x∈
,x∈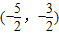 恒成立,构造函数y=-
恒成立,构造函数y=-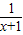 ,结合函数在
,结合函数在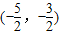 上的单调性,求出最值,可得答案.
上的单调性,求出最值,可得答案.
解答:解:(1)∵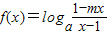 是奇函数
是奇函数
∴f(x)+f(-x)=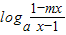 +
+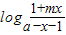 =
=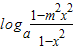 =0
=0
解得m2=1
由m≠1得m=-1. …(2分)
∴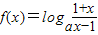 ,
,
∴g(x)=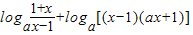
则,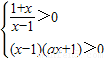
即x<-1,或x>1,
∴g(x)的定义域为{x|x<-1,或x>1}. …(6分)
(2)∵a>1
g(x)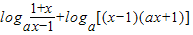 =
=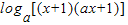 在
在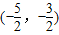 上恒为正,
上恒为正,
即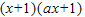 >1,…(8分)
>1,…(8分)
∴a>-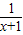 ,x∈
,x∈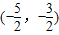 ,…(10分)
,…(10分)
由于y=-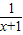 在
在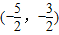 上为增函数
上为增函数
故-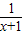 ≤-
≤-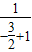 =2
=2
∴a>2
故a的取值范围为(2,+∞) …(12分)
点评:本题考查的知识点是函数恒成立问题,函数奇偶性与单调性的综合,是函数图象和性质的综合应用,难度稍大,应属于中档题.
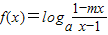 为奇函数,f(x)+f(-x)=0,结合对数的运算性质,可得m2=1,结合m≠1得m=-1,进而根据对数函数真数大于0,构造不等式组,求出函数的定义域.
为奇函数,f(x)+f(-x)=0,结合对数的运算性质,可得m2=1,结合m≠1得m=-1,进而根据对数函数真数大于0,构造不等式组,求出函数的定义域.(2)根据g(x)在
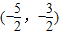 上恒为正,结合底数大于1,可得真数恒大于1,进而a>-
上恒为正,结合底数大于1,可得真数恒大于1,进而a>-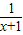 ,x∈
,x∈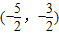 恒成立,构造函数y=-
恒成立,构造函数y=-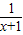 ,结合函数在
,结合函数在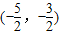 上的单调性,求出最值,可得答案.
上的单调性,求出最值,可得答案.解答:解:(1)∵
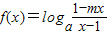 是奇函数
是奇函数∴f(x)+f(-x)=
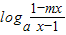 +
+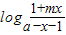 =
=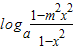 =0
=0解得m2=1
由m≠1得m=-1. …(2分)
∴
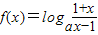 ,
,∴g(x)=
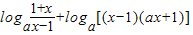
则,
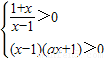
即x<-1,或x>1,
∴g(x)的定义域为{x|x<-1,或x>1}. …(6分)
(2)∵a>1
g(x)
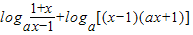 =
=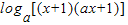 在
在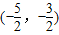 上恒为正,
上恒为正,即
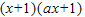 >1,…(8分)
>1,…(8分)∴a>-
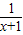 ,x∈
,x∈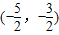 ,…(10分)
,…(10分)由于y=-
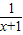 在
在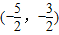 上为增函数
上为增函数故-
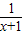 ≤-
≤-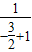 =2
=2∴a>2
故a的取值范围为(2,+∞) …(12分)
点评:本题考查的知识点是函数恒成立问题,函数奇偶性与单调性的综合,是函数图象和性质的综合应用,难度稍大,应属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
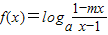 为奇函数,
为奇函数,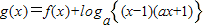 (a>1且m≠1)
(a>1且m≠1)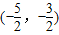 上恒为正,求a的取值范围.
上恒为正,求a的取值范围.