题目内容
已知0＜a＜b＜1，设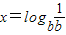
，
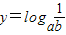，z=logab，则（ ）A．y＜x＜z
B．y＜z＜
C．x＜z＜y
D．x＜y＜z
【答案】分析：对数函数当底和真数同大于1或同大于0小于1时函数值为正，当底和真数一个大于1一个大于0小于1时函数值为负，由此得到x、y 都大于0，z小于0，再比较x和y的大小．
解答：解：∵0＜a＜b＜1
∴
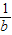＞1得到x＜0，y＜0，而当真数大于1时，函数值底大图低，∴x＜y
又∵0＜a＜1且0＜b＜1
∴z＞0
故选D．
点评：本题考查的是利用对数函数的图象比较大小的知识．
解答：解：∵0＜a＜b＜1
∴
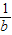＞1得到x＜0，y＜0，而当真数大于1时，函数值底大图低，∴x＜y又∵0＜a＜1且0＜b＜1
∴z＞0
故选D．
点评：本题考查的是利用对数函数的图象比较大小的知识．
练习册系列答案
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案
相关题目
已知0＜a＜b＜1，则ab，logba，log
b的关系是（ ）
| 1 |
| a |
A、log
| ||
B、log
| ||
C、logba＜log
| ||
D、ab＜log
|
已知0＜a＜b＜1，则（ ）
A、
| ||||
B、（
| ||||
| C、（lga）2＜（lgb）2 | ||||
D、
|