题目内容
5.已知f(x+1)=x-1+ex+1,则函数f(x)在点(0,f(0))处的切线l与坐标轴围成的三角形面积为$\frac{1}{4}$.分析 先求出y=f(x)=x+ex-2,再对函数进行求导,求出在x=0处的导数值即为切线的斜率值,从而写出切线方程,然后求出切线方程与两坐标轴的交点可得三角形面积.
解答 解:∵f(x+1)=x-1+ex+1,即有y=f(x)=x+ex-2,
∴y′=ex+1,∴f′(0)=2,又f(0)=-1,
即有曲线在点P(0,-1)处的切线为:y+1=2(x-0),
即2x-y-1=0,它与坐标轴的交点为:(0,-1),($\frac{1}{2}$,0),
则S=$\frac{1}{2}$×$\frac{1}{2}$×1=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题主要考查导数的几何意义,即函数在某点处的导数值等于该点的切线的斜率.属中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
10.已知函数y=$\sqrt{1-x}$+$\sqrt{x+3}$的最大值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
17.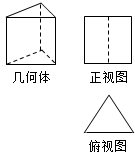 如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )
如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )
 如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )
如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )| A. | 8$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 4$\sqrt{3}$ |
14.已知f(x)是定义在R上周期为2的奇函数,当x∈(0,1)时,f(x)=3x-1,则f(log35)=( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | 4 | D. | $\frac{4}{9}$ |