题目内容
8.已知中心在原点的椭圆与双曲线的公共焦点F1、F2都在x轴上,记椭圆与双曲线在第一象限的交点为P,若△PF1F2是以PF1(F1为左焦点)为底边的等腰三角形,双曲线的离心率为2,则椭圆的离心率为$\frac{2}{5}$.分析 利用离心率的定义,及双曲线的离心率的值为3,|F1F2|=|PF2|,可求得|PF2|=2c,|PF1|=3c,利用椭圆的定义,可得结论.
解答 解:设|PF1|+|PF2|=2a′,|PF1|-|PF2|=2a,
∵△PF1F2是以PF1(F1为左焦点)为底边的等腰三角形,双曲线的离心率为3,
∴|PF2|=2c,$\frac{c}{a}$=2,
∴a=$\frac{c}{2}$,
∴|PF1|=3c,
∴5c=2a′,
∴$\frac{c}{a′}$=$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 本题考查椭圆与双曲线的几何性质,解题的关键是正确运用离心率的定义,属于中档题.

练习册系列答案
相关题目
13.散点图在回归分析过程中的作用是( )
| A. | 查找个体个数 | B. | 粗略判断变量是否线性相关 | ||
| C. | 探究个体分类 | D. | 比较个体数据大小关系 |
18.若复数(a2-2a-3)+(a+1)i是纯虚数,则实数a的值为( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1或3 |
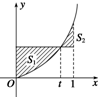 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).