题目内容
已知幂函数 为偶函数.
为偶函数.
(1)求 的解析式;
的解析式;
(2)若函数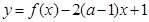 在区间(2,3)上为单调函数,求实数
在区间(2,3)上为单调函数,求实数 的取值范围.
的取值范围.
(1)  ;(2)
;(2)  或
或 .
.
解析试题分析:(1)因为是幂函数,所以 ,得出
,得出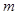 的值,在代入,看是否是偶函数;(2)将(1)的结果代入(2)式,函数在
的值,在代入,看是否是偶函数;(2)将(1)的结果代入(2)式,函数在 为单调函数,即在对称轴的某一侧,从而求出
为单调函数,即在对称轴的某一侧,从而求出 的取值范围.
的取值范围.
试题解析:解:(1)由 为幂函数知
为幂函数知 ,得
,得  或
或 3分
3分
当 时,
时, ,符合题意;当
,符合题意;当 时,
时, ,不合题意,舍去.
,不合题意,舍去.
∴ . 6分
. 6分
(2)由(1)得 ,
,
即函数的对称轴为 , 8分
, 8分
由题意知 在(2,3)上为单调函数,
在(2,3)上为单调函数,
所以 或
或 , 11分
, 11分
即 或
或 . 12分
. 12分
考点:1.幂函数的定义;2.二次函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

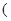 常数
常数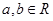 )满足
)满足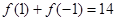 .
. 的值,并就常数
的值,并就常数 的不同取值讨论函数
的不同取值讨论函数 奇偶性;
奇偶性;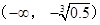 上单调递减,求
上单调递减,求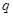 且存在递增的正整数数列
且存在递增的正整数数列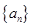 ,使得
,使得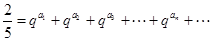 成立.
成立. 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
 ,当
,当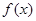 ,若在定义域存在实数
,若在定义域存在实数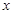 ,满足
,满足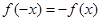 ,则称
,则称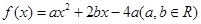 ,试判断
,试判断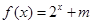 是定义在
是定义在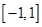 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数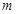 的取值范围.
的取值范围. 满足
满足 ,当
,当 时,
时, ,且
,且 .
. 的值;
的值; 的方程
的方程 有解,求
有解,求 的取值范围.
的取值范围.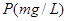 与时间
与时间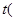 小时
小时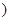 间的关系为
间的关系为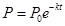 .如果在前
.如果在前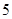 个小时消除了
个小时消除了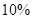 的污染物,试求:
的污染物,试求: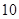 个小时后还剩百分之几的污染物?
个小时后还剩百分之几的污染物?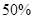 所需要的时间.(参考数据:
所需要的时间.(参考数据: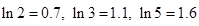 )
)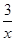 )元.
)元.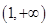 上恒取正值.
上恒取正值.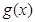 及二次函数
及二次函数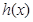 满足:
满足: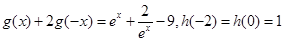 且
且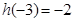 。
。 ;
;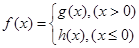 ,讨论方程
,讨论方程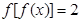 的解的个数情况.
的解的个数情况.