题目内容
20.设y=f(x)是定义在(0,+∞)上的减函数,且满足f(xy)=f(x)+f(y),f($\frac{1}{3}$)=1.(1)求f(1),f($\frac{1}{9}$),f(9)的值;
(2)若f(x)-f(2-x)<2,求x的取值范围.
分析 (1)利用赋值法即可求f(1),f($\frac{1}{9}$),f(9)的值;
(2)结合函数单调性以及抽象函数的关系将不等式进行转化即可.
解答 解:(1)令x=y=1,则f(1)=f(1)+f(1),即f(1)=0,
令x=y=$\frac{1}{3}$,则f($\frac{1}{3}$×$\frac{1}{3}$)=f($\frac{1}{3}$)+f($\frac{1}{3}$),
即f($\frac{1}{9}$)=2f($\frac{1}{3}$)=2,
令x=$\frac{1}{9}$,y=9得f($\frac{1}{9}$×9)=f($\frac{1}{9}$)+f(9),
即f(1)=f($\frac{1}{9}$)+f(9),
则f(9)=f(1)-f($\frac{1}{9}$)=0-2=-2.
(2)若f(x)-f(2-x)<2,则f(x)<f(2-x)+f($\frac{1}{9}$),
即f(x)<f($\frac{1}{9}$(2-x)),
∵y=f(x)是定义在(0,+∞)上的减函数,
∴$\left\{\begin{array}{l}{x>0}\\{2-x>0}\\{x>\frac{1}{9}(2-x)}\end{array}\right.$,即$\left\{\begin{array}{l}{x>0}\\{x<2}\\{x>\frac{1}{5}}\end{array}\right.$,即$\frac{1}{5}$<x<2,
解得$\frac{1}{5}$<x<2,
即不等式的解集为($\frac{1}{5}$,2).
点评 本题主要考查抽象函数的应用,利用赋值法是解决抽象函数的基本方法,综合考查函数的性质是应用.

练习册系列答案
相关题目
11.已知集合P={α|2kπ≤α≤(2k+1)π,k∈Z},Q={α|-4≤α≤4},则P∩Q=( )
| A. | φ | B. | {α|-4≤α≤-π,或0≤α≤π} | ||
| C. | {α|-4≤α≤4} | D. | {α|0≤α≤π} |
8.函数y=3x+log3(x+2)在[0,1]上的最大值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
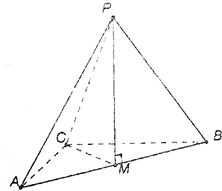 已知点P为Rt△ABC所在平面外的一点,且PA=PB=PC,M为斜边AB的中点.
已知点P为Rt△ABC所在平面外的一点,且PA=PB=PC,M为斜边AB的中点.