题目内容
若某空间几何体的三视图如图所示,则该几何体的体积是( )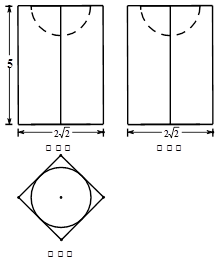
| A.20-2π | B. | C. | D. |
B
解析试题分析:由三视图可知,此几何体为底面是边长为2的正方形、高为5的正四棱柱上部去掉一个半径为1的半球,据此可计算出体积.解:由三视图可知,此几何体为底面是边长为2的正方形、高为5的正四棱柱,上部去掉一个半径为1的半球,所以其体积为V=a2h- πr3=4×5-
πr3=4×5- =
= ,故答案为B.
,故答案为B.
考点:由三视图求几何体的体积
点评:本题考查由三视图求几何体的体积,由三视图正确恢复原几何体是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个几何体的三视图如右图所示,则该几何体的体积为( )
A. | B. | C. | D. |
下列物体的三视图与物体摆放位置无关的是( )
| A.正方体 | B.正四面体 | C.正三棱锥 | D.球 |
长方体一个顶点上三条棱的长分别为3、4、5,且它的八个顶点都在同一球面上,这个球的表面积是( )
A.20 π π | B.25 π π | C.50π | D.200π |
一个几何体的三视图如图所示,则该几何体的表面积为( )
A. | B. |
C. | D. |
正方体的内切球和外接球的半径之比为
A. | B. | C. | D. |
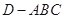 中,已知
中,已知 ,
, 平面
平面 ,
,  . 若其直观图、正视图、俯视图如图所示,则其侧视图的面积为( )
. 若其直观图、正视图、俯视图如图所示,则其侧视图的面积为( )








 B.
B. C. 6 D. 4
C. 6 D. 4