题目内容
 如图,在双曲线
如图,在双曲线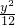 -
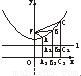
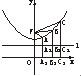
-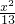 =1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.
=1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.
(1)求y1+y3的值;
(2)证明:线段AC的垂直平分线经过某一定点,并求此点坐标.
(1)解:c=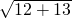 =5,故F为双曲线的焦点,设F对应准线为l,则l的方程 y=
=5,故F为双曲线的焦点,设F对应准线为l,则l的方程 y= ,离心率为e=
,离心率为e= =
= ,
,
由题设有2|FB|=|FA|+|FC|.①分别过A、B、C作x轴的垂线AA2、BB2、CC2,交l于A1、B1、C1,
则由双曲线第二定义有|FB|=e|BB1|,|FA|=e|AA1|,|FC|=e|CC1|,代入①式,得 2e|BB1|=e|AA1|+e|CC1|,
即2|BB1|=|AA1|+|CC1|.∴2(6- )=
)= +
+ ,∴y1+y3=12.
,∴y1+y3=12.
(2)证明:线段AC中点D( ,6),线段AC的斜率为
,6),线段AC的斜率为  ,
,
∴线段AC的中垂线的斜率为- ,∴线段AC的中垂线的方程为 y-6=-
,∴线段AC的中垂线的方程为 y-6=- (x-
(x- ) ①,
) ①,
又A、C在双曲线上,∴ ,
, ,相减得
,相减得  ,
,
∴x12-x32=13(y1-y3),代入①得 线段AC的中垂线的方程为 y=- x+
x+ ,
,
显然过定点(0, ).
).
分析:(1)求出焦点坐标和准线方程,依据双曲线第二定义有|FB|=e|BB1|,|FA|=e|AA1|,|FC|=e|CC1|,代入
2|FB|=|FA|+|FC|得,2|BB1|=|AA1|+|CC1|,即2(6- )=
)= +
+ ,求出y1+y3 的值.
,求出y1+y3 的值.
(2) 用点斜式求出 线段AC的中垂线的方程 为 y-6=- (x-
(x- ) ①,
) ①,
把 ,
, ,相减得
,相减得  ,
,
可得x12-x32=13(y1-y3),代入①得 y=- x+
x+ ,显然过定点(0,
,显然过定点(0, ).
).
点评:本题考查双曲线的定义和双曲线的标准方程,以及双曲线的简单性质的应用,等差数列的定义.
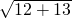 =5,故F为双曲线的焦点,设F对应准线为l,则l的方程 y=
=5,故F为双曲线的焦点,设F对应准线为l,则l的方程 y= ,离心率为e=
,离心率为e= =
= ,
,由题设有2|FB|=|FA|+|FC|.①分别过A、B、C作x轴的垂线AA2、BB2、CC2,交l于A1、B1、C1,
则由双曲线第二定义有|FB|=e|BB1|,|FA|=e|AA1|,|FC|=e|CC1|,代入①式,得 2e|BB1|=e|AA1|+e|CC1|,
即2|BB1|=|AA1|+|CC1|.∴2(6-
 )=
)= +
+ ,∴y1+y3=12.
,∴y1+y3=12.(2)证明:线段AC中点D(
 ,6),线段AC的斜率为
,6),线段AC的斜率为  ,
,∴线段AC的中垂线的斜率为-
 ,∴线段AC的中垂线的方程为 y-6=-
,∴线段AC的中垂线的方程为 y-6=- (x-
(x- ) ①,
) ①,又A、C在双曲线上,∴
 ,
, ,相减得
,相减得  ,
,∴x12-x32=13(y1-y3),代入①得 线段AC的中垂线的方程为 y=-
 x+
x+ ,
,显然过定点(0,
 ).
).分析:(1)求出焦点坐标和准线方程,依据双曲线第二定义有|FB|=e|BB1|,|FA|=e|AA1|,|FC|=e|CC1|,代入
2|FB|=|FA|+|FC|得,2|BB1|=|AA1|+|CC1|,即2(6-
 )=
)= +
+ ,求出y1+y3 的值.
,求出y1+y3 的值.(2) 用点斜式求出 线段AC的中垂线的方程 为 y-6=-
 (x-
(x- ) ①,
) ①,把
 ,
, ,相减得
,相减得  ,
,可得x12-x32=13(y1-y3),代入①得 y=-
 x+
x+ ,显然过定点(0,
,显然过定点(0, ).
).点评:本题考查双曲线的定义和双曲线的标准方程,以及双曲线的简单性质的应用,等差数列的定义.

练习册系列答案
相关题目
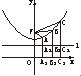 如图,在双曲线
如图,在双曲线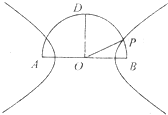 如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中心,P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.
如图,在以点O为圆心,AB为直径的半圆中,D为半圆弧的中心,P为半圆弧上一点,且AB=4,∠POB=30°,双曲线C以A,B为焦点且经过点P.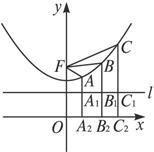
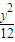 -
-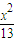 =1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.
=1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.