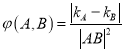题目内容
【题目】动点
到定点
的距离之比它到直线
的距离小1，设动点的轨迹为曲线
，过点
的直线交曲线于
两个不同的点，过点分别作曲线的切线，且二者相交于点
.
（1）求曲线的方程；
（2）求证：
；
（3）求
的面积的最小值.
【答案】(Ⅰ)
．(Ⅱ) 见解析；(Ⅲ)4．
【解析】
试题分析:（1）根据抛物线定义确定曲线
的方程；（2）根据导数求得切线斜率，利用点斜式写出切线方程，解方程组可得交点坐标，最后利用向量数量积为零证明结论（3）三角形高为
，根据抛物线定义求焦点弦长，根据三角形面积公式得关于斜率函数关系式，最后解函数最值得结论
试题解析：(Ⅰ)解：由已知，动点P在直线
上方，条件可转化为动点P到定点F(0，1)的距离等于它到直线
距离
∴动点P的轨迹是以F(0，1)为焦点，直线为准线的抛物线
故其方程为．
(Ⅱ)证：设直线AB的方程为：
由
得：
设A(xA，yA)，B(xB，yB)，则
由得：
，∴
∴直线AM的方程为：
①
直线BM的方程为：
②
①－②得：
，即
将
代入①得：
∴
故
∴
∴
(Ⅲ)解：由(Ⅱ)知，点M到AB的距离
∵
∴
∴当k = 0时，△ABM的面积有最小值4．
练习册系列答案
相关题目
