题目内容
3.设集合A={x∈R|2x-8=0},B={x∈R|x2-2(m+1)x+m2=0}(1)若m=4,求A∪B;
(2)若A∪B=A,求实数m的取值范围.
分析 (1)把m=4代入B中方程求出解,确定出B,求出A中方程的解确定出A,找出两集合的并集即可;
(2)由B为A的子集,分B为空集与B不为空集两种情况求出m的范围即可.
解答 解:(1)由A中方程解得:x=4,即A={4};
将m=4代入B中的方程得:x2-10x+16=0,即(x-2)(x-8)=0,
解得:x=2或x=8,即B={2,8},
则A∪B={2,4,8};
(2)∵A∪B=A,∴B⊆A或B=A,
∴当B=∅时,则有△=4(m+1)2-4m2<0,即m<-$\frac{1}{2}$;
当B=A时,则△=4(m+1)2-4m2=0,且-$\frac{-2(m+1)}{2}$=4
解得:m不存在;
故m<-$\frac{1}{2}$.
点评 此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.

练习册系列答案
相关题目
14.已知圆的方程为x2+y2=1,则圆心到直线x+y+2=0的距离为( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
11.设f(x)是定义在R上的增函数,且对于任意的x都有f(-x)+f(x)=0恒成立,如果实数a,b满足不等式组$\left\{\begin{array}{l}{f({a}^{2}-6a+23)+f({b}^{2}-8b-2)≤0}\\{f(b+1)>f(5)}\end{array}\right.$,那么a2+b2的取值范围是( )
| A. | [9,49] | B. | (17,49] | C. | [9,41] | D. | (17,41] |
18.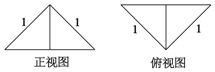 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为( )
 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{1}{4}$ |