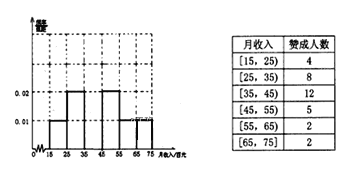
题目内容
【题目】如图,在三棱柱ABC﹣A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1 , CC1上的点,且BE=B1E,C1F= ![]() CC1 , 则异面直线A1E与AF所成角的余弦值为( )
CC1 , 则异面直线A1E与AF所成角的余弦值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解以C为原点,CA为x轴,在平面ABC中过作AC的垂线为y轴,CC1为z轴,建立空间直角坐标系, 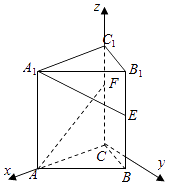
∵在三棱柱ABC﹣A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,
E,F分别是棱BB1 , CC1上的点,且BE=B1E,C1F= ![]() CC1 ,
CC1 ,
∴A1(4,0,6),E(2,2 ![]() ,3),F(0,0,4),A(4,0,0),
,3),F(0,0,4),A(4,0,0),![]() =(﹣2,2
=(﹣2,2 ![]() ,﹣3),
,﹣3), ![]() =(﹣4,0,4),
=(﹣4,0,4),
设异面直线A1E与AF所成角所成角为θ,
则cosθ= 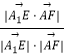 =
= ![]() =
= ![]() .
.
∴异面直线A1E与AF所成角的余弦值为 ![]() .
.
故选:D.
以C为原点,CA为x轴,在平面ABC中过作AC的垂线为y轴,CC1为z轴,建立空间直角坐标系,利用向量法能求出异面直线A1E与AF所成角的余弦值.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目