题目内容
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左右顶点为
的左右顶点为![]() ,右焦点为
,右焦点为![]() ,一条准线方程是
,一条准线方程是![]() ,点
,点![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 的两点,点
的两点,点![]() 为
为![]() 的中点.
的中点.
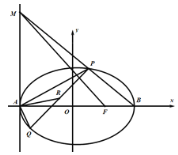
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交直线
交直线![]() 于点
于点![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)若![]() ,求直线
,求直线![]() 斜率的取值范围。
斜率的取值范围。
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 。
。
【解析】
(1)由椭圆的准线方程和右焦点![]() 可得a,c,再解出b即可;(2)由A(﹣2,0),B(2,0),设P
可得a,c,再解出b即可;(2)由A(﹣2,0),B(2,0),设P![]() ,直线PB的方程为
,直线PB的方程为![]() ,代入椭圆方程求得P的坐标,从而得M点坐标,再运用直线的斜率公式求出
,代入椭圆方程求得P的坐标,从而得M点坐标,再运用直线的斜率公式求出![]() ,
,![]() ,化简计算可得定值;(3)由
,化简计算可得定值;(3)由![]() =0,可得AP⊥AQ,即kAQkAQ=﹣1,设AP:
=0,可得AP⊥AQ,即kAQkAQ=﹣1,设AP:![]() ,代入椭圆方程3x2+4y2=12,解方程求得P的坐标,将k换为﹣
,代入椭圆方程3x2+4y2=12,解方程求得P的坐标,将k换为﹣![]() 可得Q的坐标,再由中点坐标公式可得R的坐标,再由直线的斜率公式,结合换元法和基本不等式即可得到所求范围.
可得Q的坐标,再由中点坐标公式可得R的坐标,再由直线的斜率公式,结合换元法和基本不等式即可得到所求范围.
(1)设椭圆焦距为![]() ,∵右焦点为
,∵右焦点为![]() ,∴
,∴![]() ,
,
∵一条准线方程是![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)设![]() ,则
,则![]() ∵
∵![]() ,∴
,∴![]() ,
,
又![]() ,∴直线
,∴直线![]()
![]() ,
,
又![]() ,∴
,∴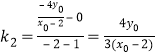 ,
,
∴![]() 。
。
(3)设直线![]() ,代入
,代入![]() ,
,
消去![]() 整理得
整理得 ![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,
,
∵![]() ,∴直线
,∴直线![]() ,
,
同理可得 ![]() ,
,
∵点![]() 为
为![]() 的中点,∴
的中点,∴![]() , 又
, 又![]() ,
,
∴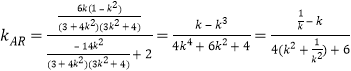 ,
,
设![]() ,则
,则![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∵![]() 或
或![]() ,∴
,∴![]() 或
或![]() ,
,
综上可知直线![]() 斜率的取值范围是
斜率的取值范围是![]() 。
。

练习册系列答案
相关题目

