题目内容
2.设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=( )| A. | {1,-3} | B. | {1,0} | C. | {1,3} | D. | {1,5} |
分析 由交集的定义可得1∈A且1∈B,代入二次方程,求得m,再解二次方程可得集合B.
解答 解:集合A={1,2,4},B={x|x2-4x+m=0}.
若A∩B={1},则1∈A且1∈B,
可得1-4+m=0,解得m=3,
即有B={x|x2-4x+3=0}={1,3}.
故选:C.
点评 本题考查集合的运算,主要是交集的求法,同时考查二次方程的解法,运用定义法是解题的关键,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
13.根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080,则下列各数中与$\frac{M}{N}$最接近的是( )
(参考数据:lg3≈0.48)
(参考数据:lg3≈0.48)
| A. | 1033 | B. | 1053 | C. | 1073 | D. | 1093 |
7.若x=-2是函数f(x)=(x2+ax-1)ex-1的极值点,则f(x)的极小值为( )
| A. | -1 | B. | -2e-3 | C. | 5e-3 | D. | 1 |
16.从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,每次抽取1张,则抽到在2张卡片上的数奇偶性不同的概率是( )
| A. | $\frac{5}{18}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{7}{9}$ |
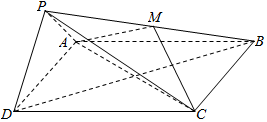 如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=$\sqrt{6}$,AB=4.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=$\sqrt{6}$,AB=4.