题目内容
已知函数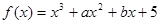 ,曲线
,曲线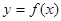 在点
在点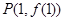 处的切线方程为
处的切线方程为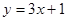 .
.
(1)求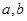 的值;
的值;
(2)求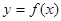 在
在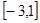 上的最大值.
上的最大值.
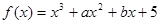 ,曲线
,曲线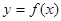 在点
在点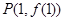 处的切线方程为
处的切线方程为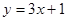 .
.(1)求
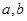 的值;
的值;(2)求
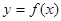 在
在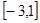 上的最大值.
上的最大值.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)将切点
 代入切线方程
代入切线方程 确定
确定 的值,求
的值,求 ,由切线方程
,由切线方程 ,可知
,可知 ,列出关于
,列出关于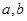 的方程组即可求解;(2)由(1)确定的
的方程组即可求解;(2)由(1)确定的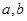 ,确定
,确定 ,用导数确定
,用导数确定 在区间
在区间 的极大值与极小值,然后比较极大值、端点值
的极大值与极小值,然后比较极大值、端点值 ,即可得到函数
,即可得到函数 在区间
在区间 的最大值.
的最大值.试题解析:(1)依题意可知点
 为切点,代入切线方程
为切点,代入切线方程 可得
可得
所以
 即
即
又由
 ,得
,得
而由切线方程
 的斜率可知
的斜率可知
所以
 即
即
联立
 7分
7分解得
 ,
, ,
, 8分
8分(2)由(1)知
 9分
9分 令
令 ,得
,得 或
或 10分
10分当
 变化时,
变化时, 的变化如下表:
的变化如下表: |  |  |  |  |  |  | 1 |
 | | + | 0 | - | 0 | + | |
 |  | 增 | 极大值 | 减 | 极小值 | 增 |  |
 的极大值为
的极大值为 极小值为
极小值为 13分
13分又
 14分
14分
 在
在 上的最大值为
上的最大值为 15分.
15分.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
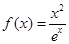 .
.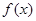 的单调区间;
的单调区间;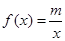 有解,求实数m的取值范围;
有解,求实数m的取值范围;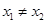 ,使
,使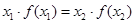 成立,求证:
成立,求证: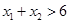 .
.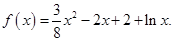
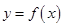 的单调区间;
的单调区间;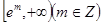 上有零点,求
上有零点,求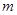 的最大值.
的最大值.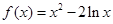 的单调递减区间是____________________.
的单调递减区间是____________________.
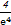
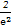
 ax2-2x(a≠0)存在单调递减区间,则实数a的取值范围是______.
ax2-2x(a≠0)存在单调递减区间,则实数a的取值范围是______. x3+bx有三个单调区间,则b的取值范围是________.
x3+bx有三个单调区间,则b的取值范围是________.