题目内容
已知函数![]()
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的极值.
的极值.
本小题主要考查函数.函数的导数.不等式等基础知识,考查运算求解能力,考查函数与方程思想.分类与整合思想,数形结合思想.化归与转化思想.满分13分.
解:函数![]() 的定义域为
的定义域为![]() ,
,![]() .
.
(Ⅰ)当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
(Ⅱ)由![]() 可知:
可知:
①当![]() 时,
时,![]() ,函数
,函数![]() 为
为![]() 上的增函数,函数
上的增函数,函数![]() 无极值;
无极值;
②当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
![]() 时,
时,![]() ,
,![]() 时,
时,![]()
![]() 在
在![]() 处取得极小值,且极小值为
处取得极小值,且极小值为![]() ,无极大值.
,无极大值.
综上:当![]() 时,函数
时,函数![]() 无极值
无极值
当![]() 时,函数
时,函数![]() 在
在![]() 处取得极小值
处取得极小值![]() ,无极大值.
,无极大值.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
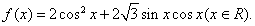
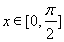
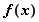

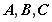
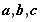
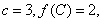
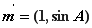
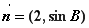
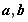

 时,求函数的最大值和最小值;
时,求函数的最大值和最小值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调减函数
上是单调减函数 .(
.( ).
). 时,求函数
时,求函数 的极值;
的极值; (2)若对
(2)若对 ,有成立,求实数
,有成立,求实数 的取值范围.
的取值范围.
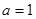 时,求
时,求 的极小值;
的极小值; ,求
,求 的最大值
的最大值 .
.