题目内容
17.下列结论判断正确的是( )| A. | 棱长为1的正方体的内切球的表面积为4π | |
| B. | 三条平行直线最多确定三个平面 | |
| C. | 正方体ABCD-A1B1C1D1中,AB与C1D1异面 | |
| D. | 若平面α⊥平面β,平面β⊥平面γ,则平面α∥平面γ |
分析 在A 中,棱长为1的正方体的内切球的表面积为π;在B中,三条平行直线最多确定三个平面;在C中,AB与C1D1平行;在D中,平面α与平面γ相交或平行.
解答 解:在A 中,棱长为1的正方体的内切球的半径为$\frac{1}{2}$,表面积为S=4$π×(\frac{1}{2})^{2}$=π,故A错误;
在B中,三条平行直线最多确定${C}_{3}^{2}=3$个平面,故B正确;
在C中,正方体ABCD-A1B1C1D1中,AB与C1D1平行,故C错误;
在D中,若平面α⊥平面β,平面β⊥平面γ,则平面α与平面γ相交或平行,故D错误.
故选:B.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意正方体、平面的基本性质及推论,面面间的位置关系的合理运用.

练习册系列答案
相关题目
8.已知集合P={0,x},Q={lnx,2},P∩Q={0},则P∪Q为( )
| A. | {0,2} | B. | {0,1,2} | C. | {1,2} | D. | {0,1} |
2.运行如图的程序,若x=2,则输出的y等于( )


| A. | 9 | B. | 7 | C. | 13 | D. | 11 |
6.函数y=$\frac{\sqrt{x+4}}{x+2}$的定义域为( )
| A. | [-4,+∞) | B. | (-2,+∞) | C. | [-4,-2) | D. | [-4,-2)∪(-2,+∞) |
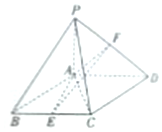 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,AB=2,PA=$\frac{{2\sqrt{3}}}{3}$,E为BC中点,F在棱PD上,AF⊥PD,点B到平面AEF的距离为$\frac{\sqrt{3}}{2}$.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,AB=2,PA=$\frac{{2\sqrt{3}}}{3}$,E为BC中点,F在棱PD上,AF⊥PD,点B到平面AEF的距离为$\frac{\sqrt{3}}{2}$.