题目内容
【题目】在①![]() ,且
,且![]() ,②
,②![]() ,且
,且![]() ,③
,③![]() ,且
,且![]() 这三个条件中任选一个,补充在下面问题中,若问题中的
这三个条件中任选一个,补充在下面问题中,若问题中的![]() 存在,求出
存在,求出![]() 和数列
和数列![]() 的通项公式与前
的通项公式与前![]() 项和;若
项和;若![]() 不存在,请说明理由.
不存在,请说明理由.
设![]() 为各项均为正数的数列
为各项均为正数的数列![]() 的前
的前![]() 项和,满足________,是否存在
项和,满足________,是否存在![]() ,使得数列
,使得数列![]() 成为等差数列?
成为等差数列?
【答案】答案不唯一,具体见解析
【解析】
由![]() ,用
,用![]() 换
换![]() 后得
后得![]() ,两式相减得
,两式相减得![]() ,若选择①,由
,若选择①,由![]() 可求得等差数列
可求得等差数列![]() 的通项公式及
的通项公式及![]() 值,前
值,前![]() 项和;若选择②,由
项和;若选择②,由![]() 得
得![]() 和
和![]() 的关系式,作为关于
的关系式,作为关于![]() 的二次方程,至少有正根,由根的分布得其条件是
的二次方程,至少有正根,由根的分布得其条件是![]() ,得出与已知矛盾的结论,说明不存在;若选择③,由
,得出与已知矛盾的结论,说明不存在;若选择③,由![]() ,同样可求
,同样可求![]() 和
和![]() .
.
解:选择①,
因为![]() ,所以
,所以![]() ,两式相减,得
,两式相减,得
![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() ,
,
因为![]() ,且
,且![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() ,
,
把![]() 代入上式,得
代入上式,得![]() ,
,
当![]() 时,由
时,由![]() 及
及![]() ,得
,得![]() ,
,
所以![]() ,
,![]() ,满足
,满足![]() ,可知数列
,可知数列![]() 是以3为首项,以2为公差的等差数列.
是以3为首项,以2为公差的等差数列.
数列![]() 的通项公式为
的通项公式为![]() ,
,
数列![]() 的前
的前![]() 项和为
项和为![]() .
.
选择②,
因为![]() ,所以
,所以![]() ,两式相减,得
,两式相减,得
![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() ,
,
因为已知数列![]() 的各项均为正数,所以
的各项均为正数,所以![]() ,
,
因为关于![]() 的一元二次方程
的一元二次方程![]() 至少存在一个正实数解的充要条件是
至少存在一个正实数解的充要条件是
![]() ,
,
解得![]() ,
,
这与已知条件![]() 矛盾,所以满足条件的
矛盾,所以满足条件的![]() 不存在.
不存在.
(注:若![]() 存在两个实数解分别为
存在两个实数解分别为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
当![]() 时,
时,![]() 的解一正一负;当
的解一正一负;当![]() 时,
时,![]() 的解一正一零;
的解一正一零;
当![]() 时,
时,![]() 的解均为正.
的解均为正.
所以方程![]() 至少存在一个正实数解,当且仅当
至少存在一个正实数解,当且仅当![]() .)
.)
选择③,因为![]() ,所以
,所以![]() ,两式相减,得
,两式相减,得
![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() ,又已知
,又已知![]() ,
,
所以![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,所以
,所以![]() ,
,
当![]() 时,由
时,由![]() 及
及![]() 得
得![]() ,
,
由![]() ,
,![]() 及
及![]() ,得
,得![]() ,
,
所以![]() 和
和![]() 满足
满足![]() ,
,
可知数列![]() 是以3为首项,以2为公差的等差数列,
是以3为首项,以2为公差的等差数列,
数列![]() 的通项公式为
的通项公式为![]() ,
,
数列![]() 的前
的前![]() 项和为
项和为![]() .
.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】某超市随机选取![]() 位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
(Ⅰ)估计顾客同时购买乙和丙的概率;
(Ⅱ)估计顾客在甲、乙、丙、丁中同时购买![]() 中商品的概率;
中商品的概率;
(Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
【题目】某大型科学竞技真人秀节目挑选选手的方式为:不但要对选手的空间感知、照相式记忆能力进行考核,而且要让选手经过名校最权威的脑力测试,120分以上才有机会入围.某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各100名,然后对这200名学生进行脑力测试.规定:分数不小于120分为“入围学生”,分数小于120分为“未入围学生”.已知男生入围24人,女生未入围80人.
(1)根据题意,填写下面的2×2列联表,并根据列联表判断是否有95%以上的把握认为脑力测试后是否为“入围学生”与性别有关;
性别 | 入围人数 | 未入围人数 | 总计 |
男生 | |||
女生 | |||
总计 |
(2)用分层抽样的方法从“入围学生”中随机抽取11名学生,求这11名学生中男、女生人数;若抽取的女生的脑力测试分数各不相同(每个人的分数都是整数),分别求这11名学生中女生测试分数平均分的最小值.
|
|
|
|
|
|
|
|
|
|
附: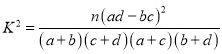 ,其中
,其中![]() .
.
