题目内容
【题目】已知点![]() ,
,![]() 是抛物线
是抛物线![]() 上的两个动点,
上的两个动点,![]() 是坐标原点,向量
是坐标原点,向量![]() ,
,![]() 满足
满足![]() .设圆
.设圆![]() 的方程为
的方程为![]() .
.
(1)证明线段![]() 是圆
是圆![]() 的直径;
的直径;
(2)当圆![]() 的圆心到直线
的圆心到直线![]() 的距离的最小值为
的距离的最小值为![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)2
【解析】
(1)根据两个向量模长之间的关系,两边平方,移项合并得到数量积为零,用坐标表示出来,根据点是圆上的点,得到线段垂直,从而数量积为零,把两个式子进行比较,整理得到结果;(2)根据两个点是抛物线.上的点,把点的坐标代入抛物线方程,整理变形得到圆心的轨迹方程,表示出圆心到直线的距离,根据二次函数的最值得到结果.
(1)∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]()
![]() ,
,
∴![]() 在圆
在圆![]() 上,
上,
同理![]() 在圆
在圆![]() 上.
上.
又∵![]() 的中点
的中点![]() 为圆
为圆![]() 的圆心,
的圆心,
∴线段![]() 是圆
是圆![]() 的直径
的直径
(2)设圆![]() 的圆心为
的圆心为![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
又![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]()
.∴![]() .
.
所以圆心的轨迹方程为:![]() .
.
设圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则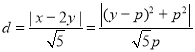 ,
,
所以当![]() 时,
时,![]() 有最小值,
有最小值,
由题设![]() ,
,
所以![]() .
.

练习册系列答案
相关题目