题目内容
【题目】
已知数列{an}和{bn}满足:a1=λ,an+1=![]() 其中λ为实数,n为正整数.
其中λ为实数,n为正整数.
(Ⅰ)对任意实数λ,证明数列{an}不是等比数列;
(Ⅱ)试判断数列{bn}是否为等比数列,并证明你的结论;
(Ⅲ)设0<a<b,Sn为数列{bn}的前n项和.是否存在实数λ,使得对任意正整数n,都有
a<Sn<b?若存在,求λ的取值范围;若不存在,说明理由.
【答案】(Ⅰ)证明见解析.
(Ⅱ)见解析.
(Ⅲ)![]()
【解析】
(Ⅰ)选择反证法来证明,假设存在推出矛盾.
(Ⅱ)用数列![]() 构造一个新数列,我们写出新数列的第
构造一个新数列,我们写出新数列的第![]() 项和第
项和第![]() 项之间的关系,发现
项之间的关系,发现![]() 的取值影响数列的性质,所以要对
的取值影响数列的性质,所以要对![]() 进行讨论.
进行讨论.
(Ⅲ)根据前面的运算写出数列的前![]() 项和,把不等式写出来观察不等式的特点,构造新函数,根据函数的最值进行验证,注意
项和,把不等式写出来观察不等式的特点,构造新函数,根据函数的最值进行验证,注意![]() 的奇偶情况要分类讨论.
的奇偶情况要分类讨论.
解:(Ⅰ)证明:假设存在一个实数![]() ,使
,使![]() 是等比数列,则有
是等比数列,则有![]() ,即
,即![]() ,矛盾.
,矛盾.
所以![]() 不是等比数列.
不是等比数列.
(Ⅱ)解:因为![]()
![]()
又![]() ,所以
,所以
当![]() ,
,![]() ,此时
,此时![]() 不是等比数列:
不是等比数列:
当![]() 时,
时,![]() ,由上可知
,由上可知![]() ,
,
![]()
![]() .
.
故当![]() 时,数列
时,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
(Ⅲ)由(Ⅱ)知,当![]() ,
,![]() ,
,![]() ,不满足题目要求.
,不满足题目要求.
![]() ,故知
,故知![]() ,于是可得
,于是可得
![]() ,
,
要使![]() 对任意正整数
对任意正整数![]() 成立,
成立,
即![]()
得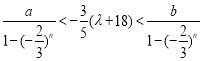
![]() ①
①
当![]() 为正奇数时,
为正奇数时,![]() ;当
;当![]() 为正偶数时,
为正偶数时,![]() ,
,
![]() 的最大值为
的最大值为![]() (1)
(1)![]() ,
,![]() 的最小值为
的最小值为![]() (2)
(2)![]() ,.
,.
于是,由①式得![]() .
.
当![]() 时,由
时,由![]() ,不存在实数满足题目要求;
,不存在实数满足题目要求;
当![]() 存在实数
存在实数![]() ,使得对任意正整数
,使得对任意正整数![]() ,都有
,都有![]() ,且
,且![]() 的取值范围是
的取值范围是![]()

【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为![]() .2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
.2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 | 服务业 |
参加用户比 |
|
|
|
|
脱贫率 |
|
|
|
|
那么![]() 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()