题目内容
在△ABC中,B=60°,最大边与最小边之比为2:1,则最大角为( )A.45°
B.60°
C.75°
D.90°
【答案】分析:根据角B=60°,可知边b既不是最大边,又不是最小边.因此设c为最大边,a为最小边,c=2a,用余弦定理计算出边b=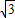 a,得到三条边的比为1:
a,得到三条边的比为1: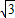 :2,最后利用余弦定理计算出cosC=0,从而得到角C=90°,即得最大角的度数.
:2,最后利用余弦定理计算出cosC=0,从而得到角C=90°,即得最大角的度数.
解答:解:∵△ABC中,B=60°,
∴边b既不是最大边,又不是最小边,
因为最大边与最小边之比为2:1,设c为最大边,a为最小边,c=2a,
根据余弦定理,得b2=a2+c2-2accos60°=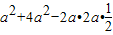 =3a2
=3a2
∴b=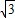 a
a
因此可得:cosC=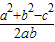 =
=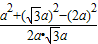 =0
=0
∵0°<C<180°
∴C=90°
∵边c为最大边⇒角C为最大角
∴最大角为90°
故选D
点评:本题以一个特殊三角形为例,在已知两边的比和夹角为60度的情况下,求三个角中最大角.着重考查了三角形中大角对大边和余弦定理等知识点,属于基础题.
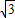 a,得到三条边的比为1:
a,得到三条边的比为1: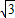 :2,最后利用余弦定理计算出cosC=0,从而得到角C=90°,即得最大角的度数.
:2,最后利用余弦定理计算出cosC=0,从而得到角C=90°,即得最大角的度数.解答:解:∵△ABC中,B=60°,
∴边b既不是最大边,又不是最小边,
因为最大边与最小边之比为2:1,设c为最大边,a为最小边,c=2a,
根据余弦定理,得b2=a2+c2-2accos60°=
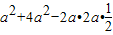 =3a2
=3a2∴b=
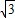 a
a因此可得:cosC=
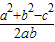 =
=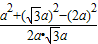 =0
=0∵0°<C<180°
∴C=90°
∵边c为最大边⇒角C为最大角
∴最大角为90°
故选D
点评:本题以一个特殊三角形为例,在已知两边的比和夹角为60度的情况下,求三个角中最大角.着重考查了三角形中大角对大边和余弦定理等知识点,属于基础题.

练习册系列答案
相关题目