题目内容
(2013•宁波二模)在△ABC中,∠B=
,|
|=3
,|
|=6,设D是AB的中点,O是△ABC所在平面内的一点,且3
+2
+
=
,则|
|的值是( )
| π |
| 6 |
| AB |
| 3 |
| BC |
| OA |
| OB |
| OC |
| 0 |
| DO |
分析:将等式3
+2
+
=
中的向量
移到右边,在两边都加上
并化简整理得
+
=
,因此
+
对应的向量
与
平行,可得点O在△ABC的中位线DF上,且到点D的距离等于
|
|,再结合|
|=6即可算出|
|的值.
| OA |
| OB |
| OC |
| 0 |
| OC |
| OB |
| OA |
| OB |
| 1 |
| 3 |
| CB |
| OA |
| OB |
| OE |
| BC |
| 1 |
| 6 |
| BC |
| BC |
| DO |
解答:解:∵3
+2
+
=
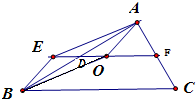
∴3
+2
=
,两边都加上
,
得3(
+
)=
,所以
+
=
∵AB中点为D,可得
+
=2
∴2
=
,可得
=
因此,点O在△ABC的中位线DF上,且满足|
|=
|
|=1
故选:B
| OA |
| OB |
| OC |
| 0 |

∴3
| OA |
| OB |
| CO |
| OB |
得3(
| OA |
| OB |
| CB |
| OA |
| OB |
| 1 |
| 3 |
| CB |
∵AB中点为D,可得
| OA |
| OB |
| OD |
∴2
| OD |
| 1 |
| 3 |
| CB |
| OD |
| 1 |
| 6 |
| CB |
因此,点O在△ABC的中位线DF上,且满足|
| OD |
| 1 |
| 6 |
| BC |
故选:B
点评:本题在△ABC中给出向量等式,求满足条件的点D到O点的距离,着重考查了三角形的中位线定理和向量的线性运算等知识,属于中档题.

练习册系列答案
相关题目
 (2013•宁波二模)如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3个小组的频数为18,则的值n是
(2013•宁波二模)如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3个小组的频数为18,则的值n是