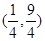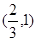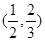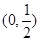题目内容
过点(0,1)与双曲线 仅有一个公共点的直线共有 ( )
仅有一个公共点的直线共有 ( )
| A.1条 | B.2条 | C.3条 | D.4条 |
D
解析试题分析:当直线的斜率不存在时,直线过双曲线 没有交点,不满足条件;
没有交点,不满足条件;
当直线的斜率存在时,设直线方程为 ,与双曲线联立
,与双曲线联立 消y得:
消y得: ,
,
当 时,方程只有一个解,满足条件,此时有2条;
时,方程只有一个解,满足条件,此时有2条;
当 时,由
时,由 得
得 ,此时也有2条。
,此时也有2条。
综上,满足条件的直线共有4条。
考点:直线与双曲线的位置关系。
点评:本题主要考查直线和双曲线的位置关系,双曲线的渐近线的性质。注意考虑二次项的系数是否为0,这是解题的易错点。

练习册系列答案
相关题目
抛物线 的焦点坐标是( )
的焦点坐标是( )
| A.(2,0) | B.(- 2,0) | C.(4,0) | D.(- 4,0) |
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B.(1,0) | C.(0,- ) ) | D.(- ,0) ,0) |
椭圆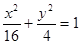 上有两点P、Q ,O为原点,若OP、OQ斜率之积为
上有两点P、Q ,O为原点,若OP、OQ斜率之积为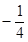 ,
, 等于( )
等于( )
| A. 4 | B. 64 | C. 20 | D.不确定 |
已知椭圆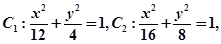 则
则
A. 与 与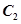 顶点相同. 顶点相同. | B. 与 与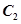 长轴长相同. 长轴长相同. |
C. 与 与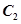 短轴长相同. 短轴长相同. | D. 与 与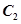 焦距相等. 焦距相等. |
 中
中 ,点
,点 的斜坐标定义为:“若
的斜坐标定义为:“若 (其中
(其中 分别为与斜坐标系的
分别为与斜坐标系的 轴,
轴, 轴同方向的单位向量),则点
轴同方向的单位向量),则点 ”.若
”.若 且动点
且动点 满足
满足 ,则点
,则点 在斜坐标系中的轨迹方程为( )
在斜坐标系中的轨迹方程为( )



 分别为双曲线
分别为双曲线 的左、右焦点,
的左、右焦点, 为双曲线左支上的一点,若
为双曲线左支上的一点,若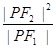 的值为
的值为 ,则双曲线离心率的取值范围是( )
,则双曲线离心率的取值范围是( )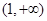




 的焦点F恰好是曲线
的焦点F恰好是曲线 的右焦点,且
的右焦点,且 交点的连线过点F,则曲线
交点的连线过点F,则曲线 的离心率为
的离心率为
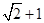


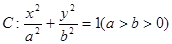 的左顶点
的左顶点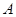 的斜率为
的斜率为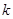 的直线交椭圆
的直线交椭圆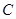 于另一个点
于另一个点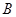 ,且点
,且点 轴上的射影恰好为右焦点
轴上的射影恰好为右焦点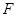 ,若
,若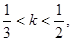 则椭圆离心率的取值范围是( )
则椭圆离心率的取值范围是( )