Question

已知△ABC的三个内角A、B、C满足A+C=2B.

，求cos的值.

Answer 1

cos

解析:

解法一:由题设条件知B=60°，A+C=120°.

设α=，则A－C=2α，可得A=60°+α，C=60°－α，

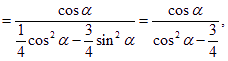
依题设条件有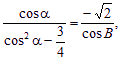

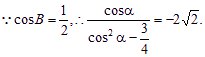
整理得4cos²α+2cosα－3=0(M)

(2cosα－)(2cosα+3)=0，∵2cosα+3≠0，

∴2cosα－=0. 从而得cos.

解法二:由题设条件知B=60°，A+C=120°

                           ①，

把①式化为cosA+cosC=－2cosAcosC               　　       ②，

利用和差化积及积化和差公式，②式可化为

      　 ③， 

将cos=cos60°=，cos(A+C)=－代入③式得 

                                   　　　④

将cos(A－C)=2cos²()－1代入 ④:

4cos²()+2cos－3=0，(*)，