题目内容
11.三棱锥P-ABC的四个顶点都在球O的球面上,已知PA,PB,PC两两垂直,且PA=1,PB+PC=4,则当三棱锥的体积最大时,球O的表面积为9π.分析 当且仅当PB=PC=2时,三棱锥的体积最大,如图所示,将P-ABC视为正四棱柱的一部分,求出△ABC外接圆的半径,即可求出球的表面积.
解答 解:由题意,V=$\frac{1}{3}$•$\frac{1}{2}$•1•PB•PC≤$\frac{1}{12}$(PB+PC)2=$\frac{4}{3}$,
当且仅当PB=PC=2时,三棱锥的体积最大,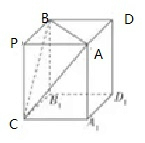
如图所示,将P-ABC视为正四棱柱的一部分,
则CD=2R,即PA2+PB2+PC2=4R2=9,可得R=$\frac{3}{2}$,
故球的表面积是:S=4π•$\frac{9}{4}$=9π,
故答案为:9π.
点评 本题考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点为F(2,0),双曲线的渐近线y=±$\sqrt{3}$x,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{13}$=1 | B. | $\frac{{x}^{2}}{13}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{3}$-y2=1 | D. | x2-$\frac{{y}^{2}}{3}$=1 |
2.已知集合A={x|log${\;}_{\frac{1}{2}}$(x+1)≥-2},B={x|$\frac{x+2}{1-x}$≥2},则 A∩B=( )
| A. | (-1,1) | B. | [0,1) | C. | [0,3] | D. | ∅ |
19.已知函数$f(x)=\left\{\begin{array}{l}{x^2}-x,x≤0\\-{2^x},x>0\end{array}\right.$,则“f(x)≤0”是“x=0”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
6.已知函数f(x)=ex+ln(x+1)的图象在(0,f(0))处的切线与直线x-ny+4=0垂直,则n的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
16.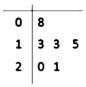 如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( )
如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( )
 如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( )
如图是一名篮球运动员在最近6场比赛中所得分数的茎叶图,则下列关于该运动员所得分数的说法错误的是( )| A. | 中位数为14 | B. | 众数为13 | C. | 平均数为15 | D. | 方差为19 |
1.已知函数f(x)=ex-$\frac{1}{{e}^{x}}$+x(e为自然对数的底数),若实数a满足f(log2a)-f(log0.5a)≤2f(1),则实数a的取值范围是( )
| A. | (-∞,$\frac{1}{2}$)∪(2,+∞) | B. | (0,$\frac{1}{2}$]∪[2,+∞) | C. | [$\frac{1}{2}$,2] | D. | (0,2] |