Question

【题目】在平面直角坐标系xOy中，已知椭圆C：的离心率，F1，F2分别为左、右焦点，过F1的直线交椭圆C于P，Q两点，且的周长为8.

（1）求椭圆c的方程；

（2）设过点M(3,0)的直线交椭圆C于不同两点A，B，N为椭圆上一点，且满足（O为坐标原点），当时，求实数t的取值范围.

Answer 1

【答案】（1）；（2）

【解析】

（1）利用已知条件，求出a，b，即可得到椭圆方程;（2）设A（x1，y1），B（x2，y2），N（x，y），AB的方程为y=k（x﹣3），联立直线和椭圆，整理得（1+4k2）x2﹣24k2x+36k2﹣4=0．利用判别式以及韦达定理，结合=t（x，y），求出N的坐标，代入椭圆方程，利用弦长公式，化简不等式，求出K的范围，然后求解t的范围．

（1）∵，∴.

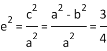又∵，∴，∴，∴椭圆的方程是.

（2）设，，，的方程为，

由，整理得.

由，得.

∵，，

∴ ，

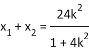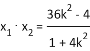则， .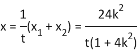

由点在椭圆上，得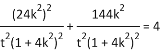，化简得. ①

又由，即，

将，代入得，

化简，得，则，，∴. ②

由①，得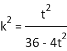，联立②，解得.

∴或，即.