题目内容
17．若a和b均为非零实数，则下列不等式中恒成立的是 （ ）| A． | $\frac{{{a^2}+{b^2}}}{2}≥{（\frac{a+b}{2}）^2}$ | B． | $\frac{b}{a}+\frac{a}{b}≥2$ | C． | $（a+b）（\frac{1}{a}+\frac{1}{b}）≥4$ | D． | $\frac{|a+b|}{2}≥\sqrt{\;|ab|}$ |
分析 利用基本不等式的使用法则“一正二定三相等”即可判断出．
解答 解：A．∵$\frac{{a}^{2}+{b}^{2}}{2}$-$（\frac{a+b}{2}）^{2}$=$\frac{（a-b）^{2}}{4}$≥0，∴$\frac{{a}^{2}+{b}^{2}}{2}$≥$（\frac{a+b}{2}）^{2}$，正确；
B．ab＜0不成立；
C．ab＜0，且a+b与$\frac{1}{a}+\frac{1}{b}$异号不成立；
D．ab＜0不成立．
故选：A．
点评 本题考查了基本不等式的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$的离心率为$\frac{\sqrt{3}}{2}$，右焦点到右准线的距离为$\frac{\sqrt{3}}{3}$．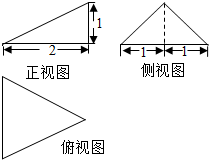
某三棱锥的三视图如图所示，则该三棱锥的4个面中，直角三角形的个数是1个，它的表面积是21．