Question

(08年海淀区期中练习理)（14分）

如图，四棱锥中，⊥底面，   ⊥．底面为梯形，，.，点在棱上，且．

（Ⅰ）求证：平面⊥平面；

（Ⅱ）求证：∥平面；

（Ⅲ）求二面角的大小．

Answer 1

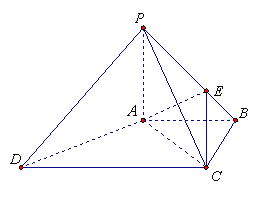
解析：证明：（Ⅰ）∵PA⊥底面ABCD，

∴．

又AB⊥BC，，

∴⊥平面．                 2分

又平面，

∴平面⊥平面．           4分

 

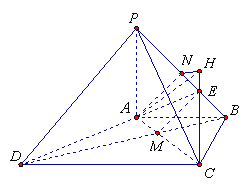
（Ⅱ）∵PA⊥底面ABCD，

∴AC为PC在平面ABCD内的射影．

又∵PC⊥AD，

∴AC⊥AD．                                                      5分

在梯形中，由AB⊥BC，AB=BC，得，

∴．

又AC⊥AD，故为等腰直角三角形．

∴．

连接，交于点，则       7分

在中，，

∴

又PD平面EAC，EM平面EAC，

∴PD∥平面EAC．                                               9分

 

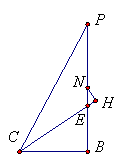
（Ⅲ）在等腰直角中，取中点，连结，则．

∵平面⊥平面，且平面平面=，

∴．

在平面内，过作直线于，连结，由于是在平面内的射影，故．

∴就是二面角A―CE―P的平面角．                          12分

在中，设，则，，，，

由，可知：∽，

∴

代入解得：．

在中，，∴．       13分

即二面角A―CE―P的大小为．                       14分

解法二：

（Ⅱ）以为原点，所在直线分别为轴、轴，如图建立空间直角坐标系．

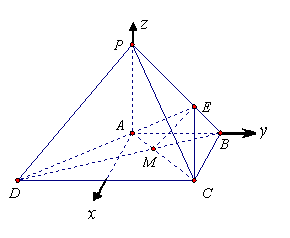
设，则，，，，.

5分

设，则

，

，

∴，解得：．

．

连结，交于点，

则.7分

在中，，

∴．

又PD平面EAC，EM平面EAC，

∴PD∥平面EAC．                                               9分

（Ⅲ）设为平面的一个法向量，则，

∴

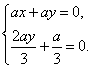
解得：，∴．                        11分

设为平面的一个法向量，则，

又，，∴

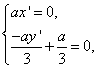
解得：，∴．                             12分

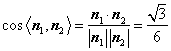．                                     13分

∴二面角A―CE―P的大小为．                            14分