题目内容
已知函数 是函数
是函数![]() 的极值点。
的极值点。
(Ⅰ)当![]() 时,求a的值,讨论函数
时,求a的值,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)当![]() R时,函数
R时,函数![]()
![]() 有两个零点,求实数m的取值范围.
有两个零点,求实数m的取值范围.
(Ⅲ)是否存在这样的直线![]() ,同时满足:
,同时满足:
①![]() 是函数
是函数![]() 的图象在点
的图象在点![]() 处的切线
处的切线
②![]() 与函数
与函数![]() 的图象相切于点
的图象相切于点![]() ,如果存在,求实数b的取值范围;不存在,请说明理由。
,如果存在,求实数b的取值范围;不存在,请说明理由。
解:(1)![]() ,
,
![]() . ....1分
. ....1分
由已知得,![]()
![]() 解得a=1. ……2分
解得a=1. ……2分
![]()
![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .又
.又![]() , ....3分
, ....3分
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减. ………4分
上单调递减. ………4分
(2)由(1)知,当![]() 时,
时,![]() 单调递减,
单调递减,![]()
当![]() ,
,![]() 单调递增,
单调递增,![]() . ………………2分
. ………………2分
要使函数![]()
![]() 有两个零点,则函数
有两个零点,则函数![]() 的图象与直线
的图象与直线![]() 有两个不同的交点.
有两个不同的交点.
①当![]() 时,m=0或
时,m=0或![]() ; ....3分
; ....3分
②当b=0时,![]() ; ....4分
; ....4分
③当![]() . ....5分
. ....5分
(3)假设存在, ![]() 时,
时,![]()
![]()
函数![]() 的图象在点
的图象在点![]() 处的切线
处的切线![]() 的方程为:
的方程为:![]() ....1分
....1分
![]() 直线
直线![]() 与函数
与函数![]() 的图象相切于点
的图象相切于点![]() ,
,
![]() ,
,![]() ,所以切线
,所以切线![]() 的斜率为
的斜率为![]()
所以切线![]() 的方程为
的方程为![]()
即![]() 的方程为:
的方程为:![]() …………2分
…………2分
得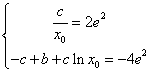
![]()

得![]() 其中
其中![]() ....3分
....3分
记![]() 其中
其中![]()
![]()
令![]() ....4分
....4分
|
|
| 1 |
|
|
| + | 0 | - |
|
|
| 极大值 |
|
又![]() ,
,![]()
![]()
所以实数b的取值范围的集合:![]() …………5分
…………5分

 53随堂测系列答案
53随堂测系列答案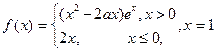 是函数
是函数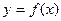 的极值点.
的极值点.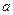 的值;
的值;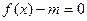 有两个不相等的实数根,求实数m的取值.
有两个不相等的实数根,求实数m的取值.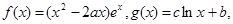
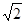 是函数
是函数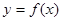 的极值点,其中
的极值点,其中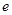 是自然对数的底数.
是自然对数的底数.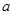 的值;
的值;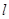 同时满足:
同时满足: 处的切线,
处的切线,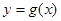 的图象相切于点
的图象相切于点 .
.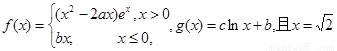 是函数
是函数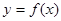 的极值点。
的极值点。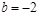 时,求a的值,讨论函数
时,求a的值,讨论函数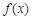 的单调性;
的单调性;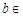 R时,函数
R时,函数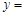
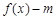 有两个零点,求实数m的取值范围.
有两个零点,求实数m的取值范围.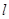 ,同时满足:
,同时满足: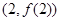 处的切线
处的切线  与函数
与函数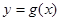 的图象相切于点
的图象相切于点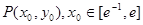 ,
, 是函数
是函数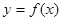 的极值点.
的极值点.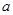 的值;
的值;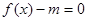 有两个不相等的实数根,求实数m的取值.
有两个不相等的实数根,求实数m的取值.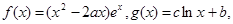
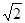 是函数
是函数 的极值点,其中
的极值点,其中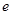 是自然对数的底数。
是自然对数的底数。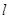 同时满足:
同时满足: 处的切线 ,
处的切线 , 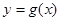 的图象相切于点
的图象相切于点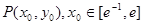 ,求实数b的取值范围
,求实数b的取值范围