题目内容
已知函数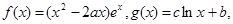
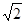 是函数
是函数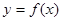 的极值点,其中
的极值点,其中
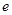 是自然对数的底数.
是自然对数的底数.
(Ⅰ)求实数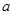 的值;
的值;
(Ⅱ)直线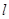 同时满足:
同时满足:
① 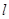 是函数
是函数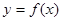 的图象在点
的图象在点 处的切线,
处的切线,
② 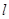 与函数
与函数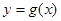 的图象相切于点
的图象相切于点 .
.
求实数b的取值范围.
【答案】
(Ⅰ)a =1(Ⅱ)① ②
②
【解析】(1)根据 建立关于a的方程,解出a值;
建立关于a的方程,解出a值;
(2)根据条件(1)可确定l:
根据条件(2) 直线 与函数
与函数 的图象相切于点
的图象相切于点 ,
,
 ,切线
,切线 的方程为
的方程为
即 的方程为:
的方程为:
然后根据两个方程为同解方程可得到方程组
然后转化为 ,利用导数确定其值域即可.
,利用导数确定其值域即可.
解:(Ⅰ)
 ……………2分
……………2分
由已知,
 得a =1
………4分
得a =1
………4分
(Ⅱ) 时,
时,

函数 的图象在点
的图象在点 处的切线
处的切线 的方程为:
的方程为: ……6分
……6分
 直线
直线 与函数
与函数 的图象相切于点
的图象相切于点 ,
,

又 ,所以切线
,所以切线 的斜率为
的斜率为
故切线 的方程为
的方程为
即 的方程为:
的方程为: ……………………8分
……………………8分
得 …………………10分
…………………10分

所以实数b的取值范围是 ……………………………………………15分
……………………………………………15分

练习册系列答案
相关题目
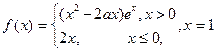 是函数
是函数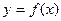 的极值点.
的极值点.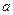 的值;
的值;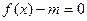 有两个不相等的实数根,求实数m的取值.
有两个不相等的实数根,求实数m的取值.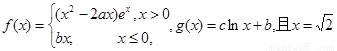 是函数
是函数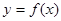 的极值点。
的极值点。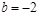 时,求a的值,讨论函数
时,求a的值,讨论函数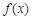 的单调性;
的单调性;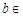 R时,函数
R时,函数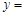
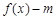 有两个零点,求实数m的取值范围.
有两个零点,求实数m的取值范围.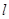 ,同时满足:
,同时满足: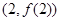 处的切线
处的切线  与函数
与函数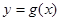 的图象相切于点
的图象相切于点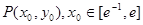 ,
, 是函数
是函数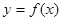 的极值点.
的极值点.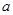 的值;
的值;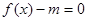 有两个不相等的实数根,求实数m的取值.
有两个不相等的实数根,求实数m的取值.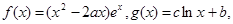
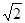 是函数
是函数 的极值点,其中
的极值点,其中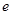 是自然对数的底数。
是自然对数的底数。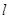 同时满足:
同时满足: 处的切线 ,
处的切线 , 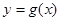 的图象相切于点
的图象相切于点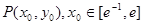 ,求实数b的取值范围
,求实数b的取值范围