题目内容
16.已知曲线y=2x2-7.(1)求曲线在点P(3,11)处的切线方程;
(2)求曲线过点P(3,9)的切线方程;
(3)求斜率为4的曲线的切线方程.
分析 (1)求导数,确定切线的斜率,即可求曲线在点P(3,11)处的切线方程;
(2)设切点坐标,可得切线方程,将P(3,9)及y0=2x02-7代入求出切点坐标,从而可求出切线方程;
(3)利用斜率为4,求出切点坐标,即可求斜率为4的曲线的切线方程.
解答 解:(1)∵y=2x2-7,∴y′=4x,
x=3时,y′=12,∴曲线在点P(3,11)处的切线方程为y-11=12(x-3),即12x-y-25=0;
(2)∵y=2x2-7,∴y′=4x
设切点坐标为(x0,y0),则切线方程为y-y0=4x0(x-x0).
将P(3,9)及y0=2x02-7代入,可得9-(2x02-7)=4x0(3-x0),
解得x0=2或x0=4,
∴设切点坐标为(2,1)或(4,25),
∴曲线过点P(3,9)的切线方程为8x-y-15=0或16x-y-39=0;
(3)由y′=4x=4,可得x=1,∴y=-5,
∴斜率为4的曲线的切线方程为y+5=4(x-1),即4x-y-9=0.
点评 本题主要考查了利用导数研究曲线上某点切线方程,同时考查了计算能力和转化的思想,解曲线的切线问题要特别注意是“在”还是“过”点.属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
8.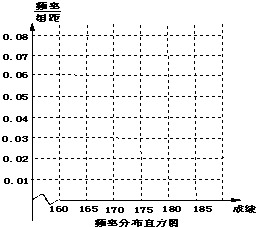 某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)由(1)所做频率分布直方图,估测出这100名学生成绩的众数、中位数、平均数;
(3)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
 某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)由(1)所做频率分布直方图,估测出这100名学生成绩的众数、中位数、平均数;
(3)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [160,165) | 5 | 0.050 |
| 第2组 | [165,170) | ① | 0.350 |
| 第3组 | [170,175) | 30 | ② |
| 第4组 | [175,180) | 20 | 0.200 |
| 第5组 | [180,185] | 10 | 0.100 |
| 合计 | 100 | 1.00 | |
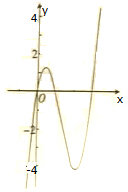 已知函数f(x)=2x(x-1)(x-3)的图象如图所示,有以下关于方程f(x)+1=0的说法:①有2个实数根;②当x>0时,有1个实数根;③当-1<x<0时,有1个实数根;④当x>1时,有1个实数根;⑤当-1<x<3时,有3个实数根.其中正确说法的序号是③⑤(填上所有正确命题的序号).
已知函数f(x)=2x(x-1)(x-3)的图象如图所示,有以下关于方程f(x)+1=0的说法:①有2个实数根;②当x>0时,有1个实数根;③当-1<x<0时,有1个实数根;④当x>1时,有1个实数根;⑤当-1<x<3时,有3个实数根.其中正确说法的序号是③⑤(填上所有正确命题的序号).