题目内容
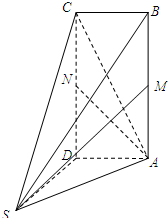如图所示，多面体ABCDS中，四边形ABCD为矩形，SD⊥AD，SD⊥AB，且AB=2AD=2，SD=| 3 |
（1）求证：SM⊥AN；
（2）求二面角A-SC-D的余弦值．
分析：（1）建立空间直角坐标系，分别求出SM，AN的方向向量，进而根据向量垂直的充要条件，得到结论；
（2）分别求出平面ASC的法向量和平面SDC的一个法向量，代入向量夹角公式可和答案．
（2）分别求出平面ASC的法向量和平面SDC的一个法向量，代入向量夹角公式可和答案．
解答：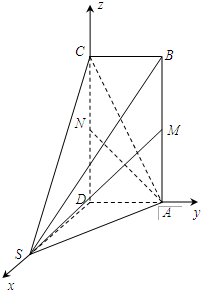
证明：（1）建立如图所示的空间直角坐标系，则
A（0，1，0），N（0，0，1），S（
，0，0），M（0，1，1），C（0，0，2），
-----------------------（3分
）
=(0，-1， 1)，
=(-
， 1， 1)，-----------------------（6分）
于是
•
=0×(-
)+(-1)×1+1×1=0，
所以SM⊥SM．-----------------------（8分）
（2）设平面ASC的法向量为
=(x，y，z)，
=(
，-1， 0)，
=(0， -1， 2)，
则
•
=
x-y=0且
•
=-y+2z=0，
令z=3，则x=2
， y=6.
=(2
， 6， 3)．-----------------------（12分）
又平面SDC的一个法向量
=(0， 1， 0)．-----------------------（13分）
设二面角A-SC-D的平面角为θ，则cosθ=|cos?
，
＞|=
=
=
，
所以二面角A-SC-D的余弦值为
．-----------------------（16分）
证明：（1）建立如图所示的空间直角坐标系，则A（0，1，0），N（0，0，1），S（
| 3 |
-----------------------（3分
）
| AN |
| SM |
| 3 |
于是
| AN |
| SM |
| 3 |
所以SM⊥SM．-----------------------（8分）
（2）设平面ASC的法向量为
| n1 |
| AS |
| 3 |
| AC |
则
| n1 |
| AS |
| 3 |
| n1 |
| AC |
令z=3，则x=2
| 3 |
| n1 |
| 3 |
又平面SDC的一个法向量
| n2 |
设二面角A-SC-D的平面角为θ，则cosθ=|cos?
| n1 |
| n2 |
| 6 | ||
1×
|
6
| ||
| 57 |
2
| ||
| 19 |
所以二面角A-SC-D的余弦值为
2
| ||
| 19 |
点评：本题考查的知识点是有空间向量求平面间的夹角，建立空间坐标系将空间线线垂直及二面角转化为向量垂直及向量夹角问题是解答的关键．
练习册系列答案
相关题目
在如图所示的多面体中，已知正方形ABCD和直角梯形ACEF所在的平面互相垂直，EC⊥AC，EF∥AC，AB=
在如图所示的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF，EF∥BC．BC=2AD=4，EF=3，AE=BE=2，G为BC的中点．
如图所示，多面体EF-ABCD中，ABCD是直角梯形，AB⊥AD，AB∥DC，∠ABC=60°，FC⊥平面ABCD，正△ADE⊥平面ABCD，