题目内容
【题目】已知圆![]() 为参数
为参数![]() 和直线
和直线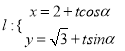
![]() 其中
其中![]() 为参数,
为参数, ![]() 为直线
为直线![]() 的倾斜角
的倾斜角![]() .
.
(1)当![]() 时,求圆上的点到直线
时,求圆上的点到直线![]() 的距离的最小值;
的距离的最小值;
(2)当直线![]() 与圆
与圆![]() 有公共点时,求
有公共点时,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)圆![]() 、直线
、直线![]() 化为直角坐标方程,求出圆心到直线的距离,再根据圆上点到直线的距离最小值一般为圆心到直线的距离减半径可得结果;(2)把圆的参数方程化为直角坐标方程,把直线的参数代入圆方程,根据判别式大于零求出倾斜角
化为直角坐标方程,求出圆心到直线的距离,再根据圆上点到直线的距离最小值一般为圆心到直线的距离减半径可得结果;(2)把圆的参数方程化为直角坐标方程,把直线的参数代入圆方程,根据判别式大于零求出倾斜角![]() 的范围.
的范围.
试题解析:(1)当![]() 时,直线
时,直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,圆
,圆![]() 的
的
圆心坐标为(1,0),圆心到直线的距离![]() ,圆
,圆![]() 的半径为1,故圆
的半径为1,故圆
上的点到直线![]() 的距离的最小值为
的距离的最小值为![]() .
.
(2)圆![]() 的直角坐标方程为
的直角坐标方程为![]() ,将直线
,将直线![]() 的参数方程代入圆
的参数方程代入圆![]() 的直
的直
角坐标方程,得![]() ,这个关于
,这个关于![]() 的一元二次方程有解,
的一元二次方程有解,
故![]() ,则
,则![]() ,即
,即![]() 或
或
![]() .又
.又![]() ,故只能有
,故只能有![]() ,
,
即![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目



