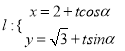题目内容
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
, ![]() ,点
,点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为2的直线![]() ,使得当直线
,使得当直线![]() 与椭圆
与椭圆![]() 有两个不同交点
有两个不同交点![]() 时,能在直线
时,能在直线![]() 上找到一点
上找到一点![]() ,在椭圆
,在椭圆![]() 上找到一点
上找到一点![]() ,满足
,满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)不存在,理由见解析.
;(2)不存在,理由见解析.
【解析】试题分析:(1)由焦点坐标可得![]() ,再根据
,再根据![]() 及点
及点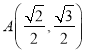 在椭圆
在椭圆![]() 上,可得
上,可得![]() ,进而可得椭圆的方程;(2)设直线
,进而可得椭圆的方程;(2)设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立可得
,与椭圆方程联立可得![]() ,与判别式为正可得
,与判别式为正可得![]() ,再根据平行四边形性质及韦达定理可得点
,再根据平行四边形性质及韦达定理可得点![]() 的纵坐标范围是
的纵坐标范围是![]() ,可判定点
,可判定点![]() 不在椭圆上,所以这样的直线
不在椭圆上,所以这样的直线![]() 不存在.
不存在.
试题解析:(1)设椭圆![]() 的焦距为
的焦距为![]() ,则
,则![]() ,
,
因此椭圆方程为![]()
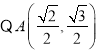 在椭圆上,
在椭圆上, 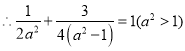 解得
解得![]()
故椭圆![]() 的方程为
的方程为![]() .
.
(2)假设存在这样的直线 设直线![]() 的方程为
的方程为![]() ,
,
设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的中点为
的中点为![]() ,
,
由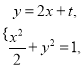 得
得![]() ,
,
所以![]() ,且
,且![]() ,则
,则![]() ,
,
![]()
![]()
由![]() 知四边形
知四边形![]() 为平行四边形,
为平行四边形,
而![]() 为线段
为线段![]() 的中点,因此,
的中点,因此, ![]() 也是线段
也是线段![]() 的中点,
的中点,
所以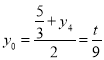 ,可得
,可得![]() ,
,
又![]() ,所以
,所以![]() ,
,
因此点![]() 不在椭圆上.
不在椭圆上.
所以这样的直线l不存在
【方法点晴】本题主要考查待定系数法求椭圆的标准方程、韦达定理以及解析几何中的存在性问题,属于难题.解决存在性问题,先假设存在,推证满足条件的结论,若结论正确则存在,若结论不正确则不存在,注意:①当条件和结论不唯一时要分类讨论;②当给出结论而要推导出存在的条件时,先假设成立,再推出条件;③当条件和结论都不知,按常规方法题很难时采取另外的途径.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目